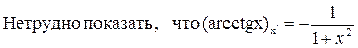Лекция 19. Вывод таблицы производных

Также как при умножении чисел используют не определение действия умножения, а таблицу умножения, так и при вычи­слении производных используют не определение производной, а таблицу производных.

Задача 1

Показать, что производная сложной функции равна произведе­нию производных составляющих функций, т.е.

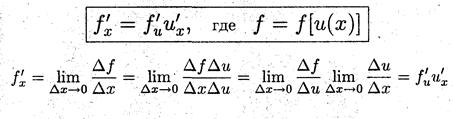
Задача2

Используя, определение производной, вычислить производные элементарных функций.

 

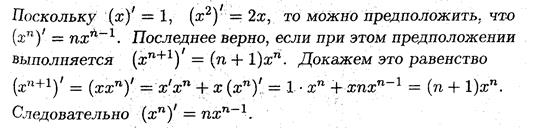
· Доказательство проведено методом математической индукции.

Пусть обе функции: прямая y=y(x) и обратная x=x(y) непрерывны и дифференцируемы на отрезке тогда

x = = = =

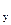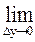
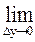
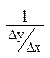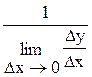Итак ,

x =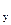

 

Продолжение задачи 2.

 

8. ,

 

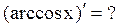
Пусть y=arcsinx, тогда x=siny

=

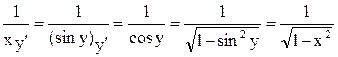
Аналогично получим, что

 

9.