Метод Сапира И.Л. -

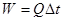а) строится вспомогательный график, где по оси ординат откладываются объемы стока в том же масштабе, что и для интегральной кривой, а по оси абсцисс - расходы и строятся две прямые: , и , где

Q - средний расход за весь период, для которого строится кривая;

- расчетный промежуток времени (месяц, декада, год...).См. рис. 1

Затем раствором циркуля с Рис. 1 (вспомогательного графика) снимается значение приращения , соответствующие

Q₁, Q₂... Q_n на расчетный период Dt и последовательно полученные DW_i наносятся на график построения интегральной кривой. соединив полученные точки и дадут интегральную кривую стока. Рис. 2

б) Для дальнейшей обработки интегральной кривой стока строится лучевой масштаб расходов (Рис. 3). Для этой цели продолжаем любой луч косого масштаба и, в произвольной точке т. В, назначаем начальную точку масштаба расходов Q=0м³/сек. Из т. В проводим перпендикулярную линию ВАС, на которой откладываем масштабные деления для расходов. Масштаб расходов выбираем в зависимости от максимального среднего месячного расхода.

(К примеру, если Q_max=247 м³/c, то 1 см = 25 м³/с).

Положение точки полюса Р лучевого масштаба определяется пересечением прямой параллельной линии ОМ через т. А соответствующей среднему расходу за весь период наблюдений.

Соединяя засечки отложенных на масштабной линейке средних расходов с точкой Р получаем лучевой масштаб графика.

 

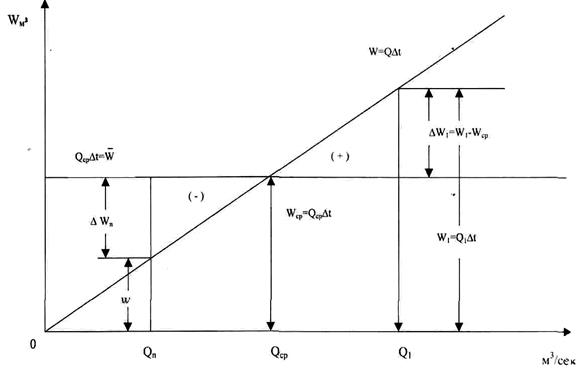
Рис.1

Рис.2 Рис.3

Проверка:

1.Полюсное расстояние можно определить и по формуле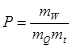, где , где

m_w, m_Q, m_t - соответственно масштабы объемов, расходов, времени.

2.Направление нулевого косого луча можно проверить по формуле:

Q_ср=tg a , откуда tg a=Q_ср , где n - масштаб времени, m - масштаб объемов.

3.Косая сетка по интегральной кривой стока строится методом соединения семейств прямых шкалы времени и шкалы объемов (к примеру: октябрю - соответствует объем W_x). Измеренный угол a должен соответствовать вычисленному углу по Формуле.