Полуцикловые неразрывные характеристики изгиба

Полуцикловые характеристики изгиба изучают, как пра­вильно, без доведения образца до разрушения и наиболее распространенной из них является жесткость, определяющая целевое на­значение материалов. Например, отдельные детали одежды долж­ны хорошо изгибаться, т. е. обладать малой жесткостью. В тоже время другие должны иметь достаточную жесткость, которая обес­печивает устойчивость отдельных деталей одежды. Под жестко­стью тела понимается его способность сопротивляться изменению формы при действии внешней силы. В теории упругости, согласно закону Гука, жесткость на изгиб В, сн см², выражается произведе­нием модуля продольной упругости Е на момент инерции сечения тела относительно нейтральной оси J

B=EJ (14. 37)

Момент инерции (J, см⁴ характеризует способность тела со­противляться изгибу в зависимости от размеров и формы попереч -

ного сечения. Модуль продольной упругости Е, сн/см² характери­зует способность тела изгибаться в зависимости от материала тела и он находиться в прямолинейной зависимости от напряжения и деформации. Для текстильных материалов, упругая деформация, возникающая при изгибе, составляет лишь небольшую долю от общей и поэтому весьма сложно определить истинную жесткость. Для расчетов используют так называемую величину условной же­сткости, В_у, мкн см². Аполитический метод расчета жесткости при изгибе, основан на приближенном решение дифференциальных уравнений линии изгиба для случая больших прогибов. При этом определяют стрелу прогиба f конца продольно расположен­ного образца (рис. 10. 10)

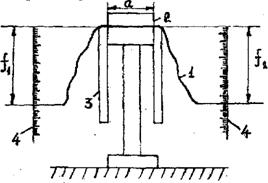
Рис. 10. 10 Схема метода определения условной жесткости тканей при изгибе

Образец 1, прямоугольной формы с длиной L располагается на горизонтальных консолях 3 в виде пластин, которые плавно опускаются. Образец прижи­мается грузом 2. После опускание пластин, концы об­разца прогибаются и по шкале 4 определяют величину прогиба f. Условную жесткость By. мкн. см², рассчиты­вают по формуле

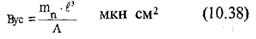
А - коэффициент, определяемый как функция относи­тельной стрелы прогиба fо

(10. 40) 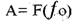(10. 41)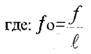

Формула 10. 40. для значений 0<fо < 0,35 имеет вид

а для 0,35 <fо < 0,8

 

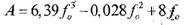(10. 42)

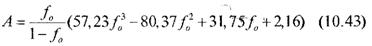
Ввиду трудоемкости расчетов, при массовых ис­пытаниях имеются специальные таблицы по которым

можно определить величину А по значениям fо. Жест­кость при изгибе может определяться так же по методу петли, весовому методу и другим, в этом случае расчеты условной жесткости проводятся но иным формулам.

Жесткость при изгибе зависит от жесткости воло­кон и нитей, от структуры изделий и в большей мере от их толщины. На жесткость сильное влияние оказывает различные виды обработок. Значения жесткости для отдельных видов изделий приведены в таблице 10. 5. Же­сткость при изгибе во многом определяет другую важ­

ную характеристику - драпируемость, способность тек­стильных изделий в подвешенном состоянии под дейст­вием собственной массы образовывать красивые, округ­лые складки. Драпируемость определяется, обычно, од­ним из двух методов:

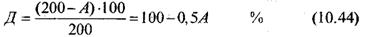
200 - ширина прямоугольного образца, мм.

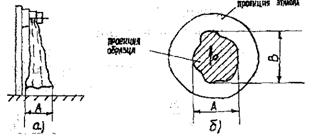
Рис. 10. 11. Схема методов определения драпируемости

- метод прямоугольных образцов, сущность кото­рого состоит в том, что прямоугольный образец нака­лывается на горизонтально расположенной игле и за­крепляется пробками. На вертикально подвешенной прямоугольной пробе образуются складки, от размеров и формы которых зависит величина А, внизу образца (рис. 10. 11а). Драпируемость определяется по формуле:

Дисковый метод. По этому вырезают пробу круг­лой формы, которую укладывают на специальный сто­лик под источник света. На листе бумаги, положенном под столиком, образуется проекция от драпируемого образца, которую обводят карандашом (рис. 10. 11. б), а затем устанавливается жесткий эталон и так же зарисо­вывают его проекцию на бумаге. Величина площади проекции образца зависит от драпируемости, и чем она меньше, тем образец лучше драпируется

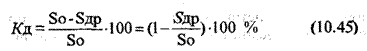где: Sдр - площадь драпируемого образца So - площадь проекции жесткого эталона

По соотношению Хо - максимальных габарит­ных размеров проекции образца (10. 11. б) в двух взаим­но перпендикулярных направлениях, можно оценивать в каком направлении лучше драпируется материал.

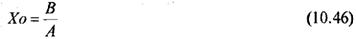
где: В - максимальный габаритный размер проекции образца вдоль изделия, мм,

А - максимальный габаритный размер проекции образца поперек изделия, мм.

Если Хо > 1,1 материал лучше драпируется в по­перечной направлении,

если Хо < 0,95 - в продольном. Значение 0,95 < Хо < 1,1 указывают на одинаковую драпируемость.

Коэффициент драпируемости Др можно прибли­женно рассчитать по эмпирической формуле в зависи­мости от показателей жесткости.

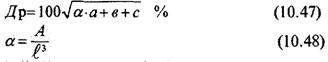
где: Л - функция относительной стрелы прогиба, формулы 10. 42,10,43

l - длина свешивающейся части образца

а, в, с - коэффициенты зависящие от величины Значение драпируемости некоторых видов изде­лий приведены в таблице 10. 5.

ГОСТ 10550-93 Материалы текстильные. Полотна. Методы определения жесткости при изгибе Дата введения в действие 01/01/1995   Количество страниц   Статус Действует   Язык Русский   Взамен ГОСТ 10550-75   Формат Электронный (pdf)   Коды ОКС 59.080.30   Коды ГКС М09

 

Настоящий стандарт распространяется на материалы для одежды - ткани, трикотажные и нетканые полотна, искусственный мех и дублированные материалы, текстильно-галантерейные изделия ( ленты и тесьму) и устанавливает следующие методы определения жесткости: определение жесткости при изгибе под действием собственной силы тяжести без принудительной деформации пробы (консольный бесконтактный метод и метод переменной длины); определение жесткости под действием сосредоточенной нагрузки с принудительной деформацией пробы (метод кольца)