Варіант 9.

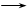
1. 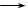Нехай точка О – точка перетину медіан трикутника АВС і АО = a, АС = b. Розкласти АВ і ВС за векторами а і b.

 

2. Трикутник АВС заданий координатами своїх вершин А(1, -2); В(4, 2);
С(13, 3). Написати рівняння прямої, яка містить бісектрису внутрішнього кута А.

 

3. Скласти рівняння прямої, яка проходить через точку перетину прямих 2х + у – 2 = 0 і х – 5у – 23 = 0 та ділить навпіл відрізок АВ, де А(5, -6);
В(-1, 4).

4. Знайти рівняння прямої, що проходить через дану пряму і

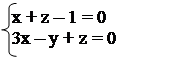парале льна прямій .

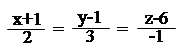5. На прямій знайти точку, яка була б рівновіддалена від

 

двох площин 12х – 9у + 20z – 1 = 0 і 16х +12у – 15z + 2 = 0.

6. З даної точки А(1, 2, -3) опустити препендикуляр на пряму , знайти його рівняння та довжину.

 

7. Знайти рівняння кола, центр якого в точці (0, 1) і яке дотикається до гіперболи 2х² – у² = 1.

 

8. Скласти рівняння хорди параболи у² = 4х, яка в точці (3, 1) ділиться навпіл.

 

9. Визначити вид поверхні та знайти її найпростіше рівняння:

3х² + 6х + 3у² – 12у + 3z² – 15z – 5 = 0.

 

10.З'ясувати геометричний зміст рівняння та побудувати ескіз: 3у² – z² = 5.