Анализ статистического ряда измерений контролируемого параметра и исключение результатов, содержащих грубые ошибки

А) Метод трех сигм (при )

Применяется для результатов измерений, распределенных по нормальному закону.

Результат содержит грубую погрешность и должен быть исключен, если выполняется следующие условия:

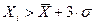
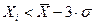
Применяется при

 

· Находим наибольшее отклонение 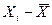; 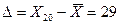, 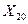=132

· Получаем новую таблицу значений без значения

Исключенное значение:

i	X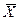

 

 

Номер измерения i	Результат измерения x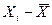
		-4
		-1
		-16
		-13
		-15
		-33
		-9
		-38
		-23
		-31
	Σ=3284		Σ=8939

 

· Рассчитываем новые значения ,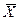

 

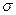
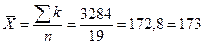
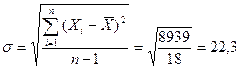
· Результат содержит грубую погрешность и должен быть исключен, если выполняется следующие условия:

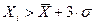
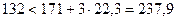
Условие не выполняется

Вывод: 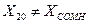, выборка не содержит грубых ошибок, никакие значения не должны быть исключены.

 

 

Б) Метод Романовского (при )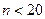

 

Предельно допустимую ошибку (максимальную крайнюю погрешность) в статистическом ряду вычисляют по формуле:

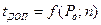- берется из справочного материала (таблица 1.5 методических указаний)

 

исключается, если выполняется неравенство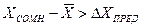

или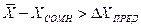

 

а) n=20; 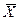=171; 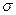=22,5;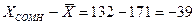

 

n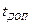
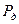
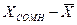
	2,62	0,9	58,95
2,78	0,95	62,55
3,08	0,99	69,3

Неравенство не выполняется

Вывод: статистический ряд не содержит результатов с грубыми погрешностями, и вычислять новые значения статистических характеристик не требуется.

 

 

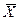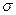б) n=10; =168; =26;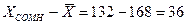

 

n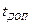
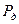
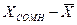
	2,29	0,9	59,54
2,41	0,95	72,28
2,62	0,99	68,12

 

Неравенство не выполняется

Вывод: статистический ряд не содержит результатов с грубыми погрешностями, и вычислять новые значения статистических характеристик не требуется.

 

в) n=5; 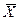=174; 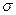=20,9;

 

n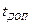
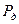
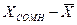
	1,87	0,9	39,083
1,92	0,95	40,128
1,97	0,99	41,173

Неравенство не выполняется

Вывод: статистический ряд не содержит результатов с грубыми погрешностями, и вычислять новые значения статистических характеристик не требуется.