Числовые характеристики непрерывной случайной величины

Математическое ожидание для непрерывно распределенных случайных величин определяется по формуле При этом интеграл, стоящий справа, должен абсолютно сходиться. Пусть X имеет плотность f(х) и j(х) - некоторая функция. Математическое ожидание величины j(X) можно вычислить по формуле

,

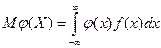если интеграл, стоящий справа, абсолютно сходится.

Дисперсия X может быть вычислена по формуле 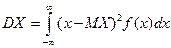, а также, как и в дискретном случае, по формул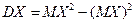е , где .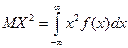

Все свойства математического ожидания и дисперсии для дискретных случайных величин, справедливы и для непрерывных случайных величин.

 

Задача 2. Для случайной величины X из задачи 1 вычислить математическое ожидание и дисперсию.

Решение.

Далее,

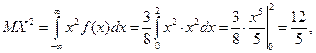и значит,

Задания:

1. Плотность распределения случайной величины X имеет вид:
   
   Вычислить константу C, функцию распределения F(x), и вероятность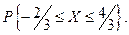

 

2. Плотность распределения случайной величины X имеет вид:

Вычислить константу C, функцию распределения F(x), и вероятность

 

1. Из колоды в 36 карт вытаскивают 3 карты. Построить функцию распределения для случайной величины X равной числу вытащенных червовых карт.

 

4. Даны законы распределения двух дискретных случайных величин X и Y

 

X					Y	-1	-2	-3
p	0,2	0,33	0,47		p	0,5	0,4	0,1

 

Построить закон распределения для дискретной случайной величины (Х+2Y). Найти для этой случайной величины математическое ожидание и дисперсию.

 

5. Найти коэффициент корреляции.

 

X\Y
	0,16	0,05	0,02
0,5	0,08	0,15	0,09
	0,01	0,28	0,16