Нелинейная Регрессия
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы: Y=ã+б/X+ε; параболы второй степени: Y= ã +бX+čX2+ε и др.
Различают два класса нелинейных регрессий:
· Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
· Регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции:
· Полиномы разных степеней – Y=б0+б1X+б2X2+б3X3+...+бkXk+ε (полином k-ой степени);
· Равносторонняя гипербола – Y= ã +б/X+ε.
К нелинейным регрессиям по оцениваемым параметрам относятся функции:
· Степенная – Y=ãXбε;
· Показательная – Y= ãбXε;
· Экспоненциальная – Y=ea+бXε.
Регрессия, нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам.
Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. При этом используется подход, именуемый «замена переменных». Суть его состоит в замене «нелинейных» объясняющих переменных новыми («линейными») переменными и сведение нелинейной регрессии к линейной. Например, в параболе второй степени: Y= ã +бX+čX2+ε заменяя переменную Х2 на Z, получим двухфакторное уравнение линейной регрессии: Y= ã +бX+čZ+ε, для оценки параметров которого, как будет показано в следующей теме, используется МНК.
Соответственно, для полинома k-ого порядка:
Y=б0+б1X+б2X2+б3X3+...+бkХk+ε,
при замене X=X1, X2=X2, X3=X3, ..., Xk=Xk получим
Y=б0+б1X1+б2X2+б3X3+...+бkXk+ε.
Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Среди нелинейной полиноминальной регрессии чаще всего используется парабола второй степени; в отдельных случаях – полином третьего порядка. Ограничение в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.
Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: приравниваем к нулю первую производную параболы второй степени: Y’=b+2cX=0 тогда Xo=-b/2c; Yo=a-b2/4c
 | |||
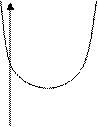 |
С>0 C<0


 Yo
Yo

 Yo
Yo

Xo Xo
Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.
Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:
åY=n*a+båX+cåX2
åYX=aåX +båX2+cåX3
åYX2=aåX2 +båX3+cåX4
Решение ее возможно методом определителей:
a=Da/D ; b=Db/D; c=Dc/D.
D - определитель системы;
Da, Db, Dc – частные определители для каждого из параметров.
При с<0 ветви параболы направлены вниз, т.е. кривая симметрична относительно высшей точки. Связь между признаками вначале прямая, а затем сменяется на обратную. Такого рода функцию можно наблюдать в экономике при изучении зависимости заработной платы работников физического труда от возраста – с увеличением возраста повышается заработная плата ввиду одновременного увеличения опыта и повышения квалификации работника. Однако с определенного возраста ввиду старения организма и снижения производительности труда дальнейшее повышение возраста может приводить к снижению заработной платы работника.
При c>0 ветви параболы направлены вверх, т.е. кривая симметрична относительно своей низшей точки. Связь между признаками вначале обратная, а затем сменяется на прямую. Так, если в зависимости от объема выпуска продукции (Х) затраты на производство (Y) характеризуются уравнением : Y’=1200 – 60X+ 2X2, то наименьшие затраты достигаются при выпуске продукции Х=15 ед. (-60+2*2*Х=0) и составляют Y’=1200-60*15+2*152=750д.е.
Ввиду симметричности кривой парабола второй степени далеко не всегда пригодна в конкретных исследованиях. Чаще исследователь имеет дело лишь с отдельными сегментами параболы, а не с полной параболической формой. Кроме того, параметры параболической связи не всегда могут быть логически истолкованы. Поэтому если график зависимости не демонстрирует четко выраженной параболы второй степени (нет смены направленности связи), то она может быть заменой другой нелинейной функцией, например, степенной.
Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу: Y=ã+б/X+ε. (*)
Она может быть использована как на микроуровне, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции, так и на макроуровне. Примером может служить так называемая кривая Филлипса, характеризующая нлинейное соотношение между нормой безработицы Х и процентом прироста заработной платы У. Английский экономист А.В.Филлипс, анализируя данные более чем за 100-летний период, в конце 50-х гг. ХХв. Установил обратную зависимость процента прироста заработной платы от уровня безработицы.
Для равносторонней гиперболы(*), заменив 1/Х на z, получим линейное уравнение регрессии Y= ã +бZ+ε, оценка параметров которого может быть дана МНК. Система нормальных уравнений составит:
åY=n*a+bå1/X

 åY/X=aå1/X +bå1/X2
åY/X=aå1/X +bå1/X2

 a
a
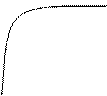
b>0 b<0
 a
a
 |
При b>0 имеем обратную зависимость, которая при х®¥ характеризуется нижней асимптотой, т.е. минимальным предельным значением У, оценкой которого служит параметр а. Так для кривой Филлипса Y’=0,00679+0,1842*1/X величина параметра а=0,00679, означает, что с ростом уровня безработицы темп прироста заработной платы в пределе стремится к нулю. Соответственно, можно определить тот уровень безработицы, при котором заработная плата оказывается стабильной и темп ее прироста равен нулю.
При b<0 имеем медленно повышающуюся функцию с верхней асимптотой при Х®¥, т.е. максимальным предельным уровнем Y, оценку которого в уравнении (*) дает параметр а.
Примером может служить взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов (или доходов). Математическое описание подобного рода взаимосвязей получило название кривых Энгеля. В 1857 г. немецкий статистик Э.Энгель на основе исследования семейных расходов сформулировал закономерность – с ростом дохода доля дохода, расходуемая на продовольствие, уменьшается. Соответственно с увеличиением дохода доля дохода, расходуемая на непродовольственные товары, будет возрастать. Однако, это увеличиение не беспредельно, ибо на все товары сумма долей не может быть больше единицы, или 100%, а на отдельные непродовольственные товары этот предел может характеризоваться величиной параметра а для уравнения вида: Y’=a-b/X, где Y' - доля расходов на непродовольственные товары; Х – доходы (или общая сумма расходов как индикатор дохода.
Соответственно, можно определить границу величины дохода, дальнейшее увеличение которого не приводит к росту доли расходов на отдельные непродовольственные товары.
Вместе с тем равносторонняя гипербола не является единственно возможной функцией для описания кривой Энгеля. В 1943 г. Уоркинг и в 1964 г. Лизер для этих целей использовали полулогарифмическую кривую
Y=ã +б*lnX+ε.
Заменив lnX на Z, опять получим линейное уравнение:
Y= ã+бZ+ε.
Данная функция, как и предыдущая, линейна по параметрам, и нелинейна по объясняющей переменной Х. Оценка параметров а и b может быть найдены с помощью МНК. Система нормальных уравнений при этом окажется следующей:
åY=n*a+bålnX
åY*lnX=aålnX +bå(lnX)2
Возможны и иные модели, нелинейные по объясняющим переменным. Например, Y=a+bÖX+ε. Соответственно система нормальных уравнений для оценки параметров составит:
åY=n*a+båÖX
åY*ÖX=aåÖX +båX
Уравнения с квадратными корнями использовались в исследованиях урожайности, трудоемкости сельскохозяйственного производства. Если нет каких-либо теоретических обоснований в использовании данного вида кривых, то основная цель подобных преобразований состоит в том, чтобы для преобразованных переменных получить более простую модель регрессии, чем для исходных данных.
Регрессия нелинейная по оцениваемым параметрам.
Данный класс нелинейных моделей подразделяется на два типа:
1) нелинейные модели внутренне линейные;
2) нелинейные модели внутренне нелинейные.
Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении спроса от цен широко используется степенная функция:
Y=ãXбε, где У – спрашиваемое количество; Х – цена; e- случайная ошибка.
Данная модель нелинейна относительно оцениваемых параметров, ибо включает параметры ã и б неаддитивно. Однако ее можно считать внутренне оинейной, ибо логарифмирование данного уравнения по основанию e приводит его к линейному виду:
LnY=ln ã + б*lnX + lnε.
Соответственно оценки параметров а и b могут быть найдены МНК. В рассматриваемой степенной функции предполагается, что случайная ошибка e мультипликативно связана с объясняющей переменной Х. Если же модель представить в виде Y=ãXб+ε, то она становится внутренне нелинейной, ибо ее невозможно преобразовать к линейному виду.
Внутренне нелинейной будет и модель вида: Y= ã + б*Xc +ε,
или модель: Y= ã *(1- 1/(1-Xб)) + ε,
ибо эти уравнения не могут быть преобразованы в уравнения, линейные по коэффициентам (параметрам).
В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят, например, экспоненциальную модель Y=ea+bX*ε, ибо логарифмируя ее по натуральному основанию, получим линейную форму модели:
lnY= ã + бX + lnε.
Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода. Модели внутренне нелинейные по параметрам могут иметь место в эконометрических исследованиях. Однако гораздо большее распространение получили модели, приводимые к линейному виду. Мы будем рассматривать только эти модели (т.е. внутренне линейные по параметрам). Решение такого типа моделей реализовано в стандартных пакетах прикладных программ. Среди них, в частности, можно назвать и обратную модель вида: Y= 1/( ã +бX+ε).
Обращая обе части равенства, получим линейную форму модели для переменной 1/Y: 1/Y= ã +бX+ε.
Приводима к линейному виду и логистическая функция:
Y= ã /(1+бe-cX+e) или Y’= a/(1+be-cX).
Обращая обе части равенства, получим: 1+be-cX+e= a /Y’.
Вычитая 1, имеем: be-cX+e= a/Y’-1.
Прологарифмировав обе части по натуральному основанию, получим уравнение линейной формы: ln b – c*lnX + ε= ln (a/Y-1) или
Z=B-c*X +ε , где z=ln(a/Y-1) и B=lnb.
Применение МНК для оценки параметров нелинейных моделей внутренне линейных.
В моделях нелинейных по оцениваемым параметрам, но приводимым к линейному виду, МНК применяется к преобразованным уравнениям. Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия å(Y-Y’)2®min, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т.е. lnY, 1/Y.
Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений в логарифмах: å(lnY-lnY')2®min.
Соответственно, если в линейных моделях (включая нелинейные по переменным) å(Y-Y’)=0, то в моделях, нелинейных по оцениваемым параметрам, å(lnY-(lnY)’)=0, а å(Y-anti (lnY)’)¹0. Вследствие этого оценка параметров для линеаризуемых функций МНК оказываются несколько смещенной.
Возьмем, например, показательную кривую: Y’=a*bX или равносильную ей экспоненту: Y’=еа+bX. Прологарифмировав, имеем: lnY=lna+X*lnb.
Прменяя МНК, минимизируем å(lnY-lnY')2. Система нормальных уравнений составит:
ålnY=n*lna+lnbåX
åX*lnY=lna*åX +lnbåX2
Из первого уравнения видно, что lna=ålnY/n – lnb*åX/n =ålnY/n – lnb*Xcp.
Предположим, что фактические данные сложились так, что Хср=0, тогда
lna= 1/n * ålnY или a=nÖY1*Y2*...*Yn, т.е. параметр а представляет собой среднюю геометрическую из значений переменной Y.
Между тем в линейной зависимости Y'=a+bX при Xcp=0 параметр а=åY/n=Ycp, т.е. средней арифметической. Поскольку средняя геометрическая всегда меньше средней арифметической, то и оценки параметров, полученные из минимизации å(lnY-ln*Y)2, будут несколько смещены (занижены).
Практическое применение экспоненты возможно, если результативный признак не имеет отрицательных значений. Поэтому если исследуется, например, финансовый результат деятельности предприятий, среди которых наряду с прибыльными есть и убыточные, то данная функция не может быть использована. Если экспонента строится как функция выравнивания по динамическому ряду для характеристики тенденции с постоянным темпом роста, то Y’=a*bt, где y – уровни динамического ряда; t – хронологические даты (периоды времени); параметр b означает средний за период коэффициент роста. В уравнении Y’=ea+bX этот смысл приобретает величина антилогарифма параметра b.
При исследовании взаимосвязей среди функций, использующих lnY, в эконометрике преобладают степенные зависимости – это кривые спроса и предложения, и кривые Энгеля, и производственные функции, и кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения выпуска нового вида изделий, и зависимость валового национального дохода от уровня занятости.
Для оценки параметров степенной функции Y= ã Xбε (*) применяется МНК к линеаризованному уравнению lnY=ln ã +б*lnX+lnε (**), т.е. решается система нормальных уравнений:
ålnY=n*lna+bålnX
ålnY*lnX=lna*ålnX +bå(lnX)2
Параметр b определяется непосредственно из системы, а параметр а - косвенным путем после потенциирования величины lna. Так, решая систему нормальных уравнений зависимости спроса от цен, было получено уравнение lnY=4,6593-1,1214*lnX. Если потенциировать его, получим:
Y’=e4,6593*X1,1214.
Поскольку параметр а экономически не интерпретируется, то нередко зависимость записывается в виде логарифмически линейной, т.е. lnY=4,6593-1,1214*lnX. В виде степенной функции изучается не только эластичность спроса, но и предложения. При этом обычно эластичность спроса характеризуется параметром b<0, а эластичность предложения: b>0.
В отдельных случаях может использоваться так называемая обратная функция: Y=1/( ã +б*X+ε), являющаяся разновидностью гиперболы. Но если в равносторонней гиперболе Y=ã +б/X+ε преобразованию подвергается объясняющая переменная 1/Х=z и Y= ã+z*X+ε, то для получения линейной формы зависимости в обратной модели преобразовывается Y, а именно: 1/Y=z и z= ã +б*X+ε (*). В результате обратная модель оказывается внутренне нелинейной и требование МНК выполняется не для фактических значений признака Y, а для их обратных величин 1/Y, а именно: å(z-z’)2®min. Соответственно:
å(1/Y)= åz’, но åY¹åY’.
Поскольку уравнение (*) линейно относительно величин 1/Y, то если обратные значения 1/Y имеют экономический смысл, коэффициент регрессии интерпретируется также как в линейном уравнении регрессии. Если, например, под Y подразумеваются затраты на рубль продукции, а под Х – производительность труда (выработка продукции на одного работника), то обратная величина характеризует затратоотдачу и параметр b имеет экономическое содержание – средний прирост продукции в стоимостном измерении на 1 руб. затрат с ростом производительности труда на единицу своего измерения.
Возможно и одновременное использование логарифмирования, и преобразование в обратные величины: Y=ea-bX+e. Прологарифмировав, получим: lnY=a-b/X+ε. Далее заменим 1/Х на z, и тогда для оценки параметров к линейному уравнению lnY=a-bz+ε может быть применен МНК.
При всех положительных значениях Х функция возрастает; при Х=b/2 кривая имеет точку перегиба – ускоренный рост при X<b/2 сменяется на замедленный рост при X>b/2. Подобного типа функции используются при анализе статистических данных о бюджетах потребителей, где выдвигается гипотеза о существовании асимптотического уровня расходов, об изменении предельной склонности к потреблению товара, о существовании “порогового уровня дохода” (Джонстон Дж.). В этом случае при Х®¥ Y®ea.
Y
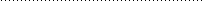
 ea
ea
 |
 0 b/2 X
0 b/2 X
Корреляция для нелинейной регрессии.
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции:
R=(s*2/s2)1/2=(1-e*2/s2)1/2=(1-å(Yi-Y’i)2/å(Yi-Ycp)2)1/2
s2 – общая дисперсия результативного признака Y;
s*2 – объясненная уравнением регрессии Y=f(X) дисперсия Y;
e*2 – остаточная (необъясненная уравнением) дисперсия признака Y.
Величина данного показателя находится в границах от 0 до 1. Чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
Парабола второй степени, как и полином более высокого порядка, при линеаризации принимает вид уравнения множественной регрессии. Если же относительно объясняющей переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции Ryx=ryz, где z – преобразованная величина признака-фактора, например z=1/X или z=lnX.
Обратимся для примера к равносторонней гиперболе Y’=a+b/X. Заменив 1/Х на z, имеем линейное уравнение Y’=a+b*Z, для которого может быть определен линейный коэффициент корреляции: ryz=b*sz/sy. Возводя данное выражение в квадрат, получим: ryz2=b2*sz2/sy2, где sz2=å(Zi-Zcp)2/n и sy2=å(Yi-Ycp)2/n.
Преобразовывая далее, придем к следующему выражению для ryz2:
ryz2= b2*å(Zi-Zcp)2/å(Yi-Ycp)2.
Как было показано ранее b2*å(Zi-Zcp)2=å(Y’i-Ycp)2 и соответственно:
ryz2=å(Y*i-Ycp)2/å(Yi-Ycp)2.
Но так как å(Yi-Ycp)2=å(Y'i-Ycp)2+å(Yi-Y'i)2 и
å(Y’i-Ycp)2=å(Yi-Ycp)2-å(Yi-Y'i)2, то
ryz2=[å(Yi-Ycp)2-å(Yi-Y’i)2]/å(Yi-Ycp)2=1-å(Yi-Y’i)2/å(Yi-Ycp)2=Ryx2
Заменив далее z на 1/X, получим Y’z=Y'x , соответственно ryz=Ryx.
Аналогичное положение имеем и для полулогарифмической кривой Y’=a+b*lnX, ибо в ней, как и в предыдущем случае, преобразования в линейный вид (z=lnX) не затрагивают зависимую переменную, и требование МНК å(Yi-Y’i)2 ® min выполнимо. То есть линейный коэффициент корреляции (ry,lnx) и индекс корреляции (RY,X) в данном случае совпадают.
Иначе обстоит дело, когда преобразования уравнения в линейную форму связаны с зависимой переменной. В этом случае линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку тесноты связи и численно не совпадает с индексом корреляции.
Так, для степенной функции Y’=a*Xb после перехода к логарифмически линейному уравнению lnY=ln a + b*ln X может быть найден линейный коэффициент корреляции не для фактических значений переменных Х и Y, а для их логарифмов, т.е. rlnX,lnY. Соответственно квадрат его значения будет характеризовать отношение факторной суммы квадратов отклонений к общей, но не для Y, а для его логарифмов:
r2lnX,lnY=å((lnYi)’-(lnY)cp)2/å(lnYi-(lnY)cp)2=
=1-å(lnYi-(lnYi)’)2/å(lnYi-(lnY)cp)2.
Между тем при расчете индекса корреляции используются суммы квадратов отклонений признака Y, а не их логарифмов. С этой целью определяются теоретические значения результативного признака, т.е. Y’, как антилогарифм рассчитанной по уравнению величины (lnY)’ и остаточная сумма квадратов как å(Yi-anti log(lnYi)’)2. Индекс корреляции определяется по формуле:
Ryx=[1-å(Yi-antilog(lnYi)’)2/å(Yi-Ycp)2].
В знаменателе расчета Ryx участвует общая сумма квадратов отклонений фактических значений Y от их средней величины, а в расчете rlnY,lnX участвует å(lnYi-(lnY)cp)2. Соответственно различаются и числители рассматриваемых показателей: å(Yi-Yi’)2=å(Yi-antilog(lnYi)’)2 – в индексе корреляции и
å(lnYi-(lnYi)’)2 – в коэффициенте корреляции.
Не совпадают данные показатели и для уравнения регрессии в виде экспоненты, ибо при преобразовании в линейную форму рассчитывается линейный коэффициент корреляции между Х и логарифмом Y, т.е. опять å(Yi-Yср)2 заменяется на å(lnYi-(lnY)ср)2 и å(Yi-anti log(lnYi)’)2 заменяется на å(lnYi-(lnYi) ')2.
При использовании в преобразовании нелинейных соотношений в линейную форму обратных значений результативного признака, т.е. 1/Y, индекс корреляции Ryx также не будет совпадать с линейным коэффициентом корреляции. В этом случае при определении индекса корреляции практически используется формула: Ryx=Ö1-å[Yi-1/(1/Y)’]2 / å[Yi-Ycp]2, т.е. теоретические значения Y' определяются не непосредственно по данным Y и X, а на основе уравнения: 1/Y=a+bX, которое может быть дополнено линейным коэффициентом корреляции между X и 1/Y.
Вследствие близости результатов и простоты расчета с использованием компьютерных программ для характеристики тесноты связи по нелинейным функциям широко используется линейный коэффициент корреляции. Несмотря на близость значений Ryx и rlnY,lnX или Ryx и rlnY,X в нелинейных функциях с преобразованием значений признака Y, следует помнить, что если при нелинейной зависимости признаков один и тот же коэффициент корреляции характеризует регрессию как Y'=a+bX, так и X'=A+B*Y, так как ry,x=rx,y, то при криволинейной зависимости Ryx для функции Y'=f(X) не равен Rxy для регрессии X'=j(Y).
Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то R2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R2 для нелинейных связей называют индексом детерминации.
Оценка существенности индекса корреляции производится также как и оценка надежности коэффициента корреляции.
Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F–критерию Фишера:
F= R2*(n-h)/[(1- R2)*(h-1)],
R2 – индекс детерминации;
n- число наблюдений;
h- число параметров в уравнении.
Величина (h-1) характеризует число степеней свободы для факторной суммы квадратов, а (n-h) – число степеней свободы для остаточной суммы квадратов.
Для степенной функции Y'=a*Xb (h-1)=1 и форма F-критерия примет тот же вид, что и при линейной зависимости: F= R2*(n-2)/(1- R2).
Для параболы второй степени: Y'= a+bX+cX 2 h-1=2 и F= R2*(n-3)/[2*(1- R2)].
Расчет F-критерия можно вести и в таблице дисперсионного анализа результатов регрессии, как это было показано для линейной регрессии.
Индекс детерминации R2 можно сравнивать с коэффициентом детерминации r2 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации r2 меньше индекса детерминации R2. Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если величина (R2- r2) не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия R2, вычисленных по одним и тем же исходным данным, через t– критерий Стьюдента: t=(R2- r2) /mR-r.
Где mR-r – ошибка разности между R2 и r2 определяемая по формуле:
mR-r=2Ö[( R2- r2)-( R2- r2)2*(2-( R2+r2))]/n.
Если tфактич>tтабл, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически если величина t<2, то различия между R и r несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.