ПРОДОЛЖИТЕЛЬНОСТЬ ЖИЗНИ

 

Разработка теории страхования жизни должна начинаться с разработки систем понятий о продолжительности жизни. Так как о продолжительности жизни отдельно взятого человека нельзя сказать ничего определенного, то можно говорить о том, что продолжительность жизни является случайной величиной X. Поэтому необходимо сначала определить закон распределения вероятностей случайной величины

В теории вероятностей этот закон распределения задается функцией распределения вероятностей

 

,

 

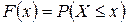которая определяет вероятность того, что продолжительность жизни 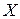не превзойдет некоторого значения .

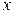В страховой математике в качестве первичной характеристики продолжительности жизни применяют так называемую функцию выживания

 

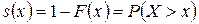, (1)

 

которая определяет вероятность того, что случайная величина X принимает значения, большие x, то есть случайно взятый человек уже прожил, по крайней мере, 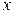лет.

Исходя из свойств функции распределения вероятностей, можем записать следующие свойства функция выживания:

 

1) ,

2) ,

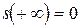3) 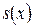- непрерывная и строго убывающая функция.

 

Статистическим аналогом функции выживания s(x) является величина 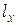, равная среднему числу лиц, доживших до x лет:

 

, (2)

 

где l₀ - количество новорожденных человек. Тогда

 

 

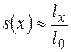
характеризует среднюю долю живых представителей некоторой фиксированной группы новорожденных к моменту времени x.

Еще одной характеристикой продолжительности жизни 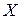служит плотность распределения вероятностей 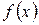, определяемая как:

 

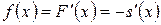. (3)

 

Статистическим аналогом плотности распределения служит величина 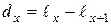- число представителей исходной группы, умерших в возрасте от x до 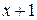лет, а именно:

.
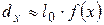