Занятие №42. Решение логарифмических неравенств.
Опр.Неравенство вида 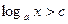 называется логарифмическим.
называется логарифмическим.
Для решения правую и левую часть уравнения надо представить в виде логарифмов с одинаковыми основаниями:  . Далее можно перейти к неравенству относительно подлогарифмических выражений, причем, если а>0, то знак неравенства не меняется, а если a<0, то меняется на противоположный. После решения неравенства необходимо найти пересечение с ОДЗ (x>0)!
. Далее можно перейти к неравенству относительно подлогарифмических выражений, причем, если а>0, то знак неравенства не меняется, а если a<0, то меняется на противоположный. После решения неравенства необходимо найти пересечение с ОДЗ (x>0)!
В общем случае логарифмическое неравенство нужно привести к виду:  . Обратите внимание, что справа и слева находится одно слагаемое, коэффициент перед которым равен единице.
. Обратите внимание, что справа и слева находится одно слагаемое, коэффициент перед которым равен единице.
Далее можно перейти к решению неравенства относительно подлогарифмических выражений и проверке условий ОДЗ:
1) если а>0
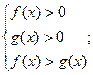
2) если а>0
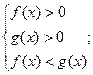
Прим.1: 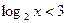
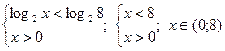
Прим.2: 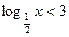
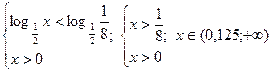
1. Решить неравенство:
1)  ; 2)
; 2) 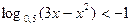 ; 3)
; 3)  ; 4)
; 4) 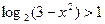 ;
;
2. Решить неравенство:
1) 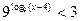 ; 2)
; 2) 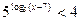 ; 3)
; 3) 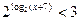 ; 4)
; 4) 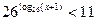
3. Решить неравенство:
1)  ;
;
2) 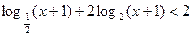 ;
;
3) 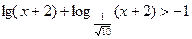 ;
;
4) 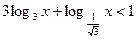 ;
;
Дополнительные задания:
Решить неравенство:
1) 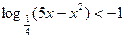 ; 2)
; 2) 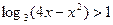 ;
;
Решить неравенство:
1) 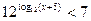 ; 2)
; 2)  ;
;
Решить неравенство:
1) 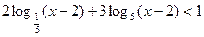 ;
;
2)  ;
;
Домашнее задание:
1. Решить неравенство:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
2. Решить неравенство:
1) 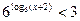 ; 2)
; 2)  ;
;
3. Решить неравенство:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;