Тема: «Расчет напряженности по теореме Гаусса»

 

1. Построить на одном графике кривые зависимости напряженности Е электрического поля от расстояния r в интервале 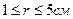через каждый 1 см, если поле образовано: а) точечным зарядом q = 33,3 нКл; б) бесконечно длинной заряженной нитью с линейной плотностью заряда τ = 1,67 мкКл/м; в) бесконечно протяженной плоскостью с поверхностной плотностью заряда σ = 25 мкКл/м².

 

2. На каком расстоянии r₁ от центра шара радиусом R, равномерно заряженного по объему, напряженность электрического поля Е равна напряженности поля вне шара на расстоянии r₂ = 2R?

 

3. Оценить среднюю плотность электрических зарядов в атмосфере, если известно, что напряженность электрического поля вблизи поверхности Земли Е₀ = 100 Н/Кл, а на высоте h = 1,5 км напряженность поля Е = 25 Н/Кл. Радиус Земли .

 

4. В равномерно заряженном шаре радиуса R вырезали сферическую полость радиуса r, центр которой находится на расстоянии l от центра шара. Объемная плотность заряда ρ. Найдите напряженность электрического поля вдоль прямой, проходящей через центр полости и центр шара. Докажите, что электрическое поле в полости однородно.

 

5. В равномерно заряженной бесконечной пластине вырезали сферическую полость так, как показано на рисунке. Толщина пластины h, объемная плотность заряда ρ. Чему равна напряженность электрического поля в точке А? в точке В? Найдите зависимость напряженности электрического поля вдоль прямой ОА от расстояния до точки О.

 

6. При пересечении двух шаров радиуса R, центры которых находятся на расстоянии l друг от друга, образуются два «полумесяца», равномерно заряженных разноименными электрическими зарядами. Объемная плотность электрического заряда слева –ρ, справа +ρ. Докажите, что электрическое поле в области пересечения шаров однородно. Найдите напряженность этого поля.

Волькенштейн №9.21, 3800 задач №11.117, 11.115, Савченко №6.2.13, 6.2.12, 6.2.14

Ответы:

1. квадратичная гипербола, гипербола, константа

2.

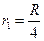
3.

4. в любой точке внутри полости, направлена вдоль прямой, соединяющей центры шара и полости

Вне полости

при

при

при

5. , ,

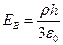6.