Комбинация нормального и экспоненциального распределений

У большинства технических объектов, вступивших в период износа, помимо износовых отказов возникают и внезапные отказы. Если считать эти два вида отказов независимыми, тогда интенсивность отказов объекта в период износа определяется как сумма

λ=λ_в + λ_и (4.11)

где λ_в— интенсивность внезапных отказов; λ_и— интенсивность износовых отказов. Вероятность безотказной работы такого объекта

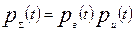(4.12)

Обычно в случае внезапных отказов распределение времени безотказной работы описывается экспоненциальным законом, т. е.

(4.13)

а в случае отказов износовых — нормальным:

 

р_и(t)= =

 

Тогда

.

Поскольку λ_Σ =f_в(t)/p_в(t) + f_и(t)/p_и(t),

то λ_Σ(t)=λ_в(t)+ . (4.15)

Перемножая (4.14) и (4.15), получаем выражение обобщенной плотности вероятности:

(4.16)

 

Такое распределение иногда называют нормально-экспоненциальным (рис. 4.1): кривая 1 соответствует случаю, когда превалируют внезапные отказы, кривая 2 — превалируют износовые отказы.

f_Σ(t) 1

 

0 t

Интегрирование (4.14) от 0 до ∞ при малом коэффициенте вариации позволяет получить приближенное выражение средней наработки на отказ:

(4.17)

 

В данном случае коэффициент вариации k_e = σ[t]/M[t] есть безразмерная мера рассеивания распределения времени безотказной работы объекта.