Краткие теоретические сведения
Лабораторная работа № 1
Тема: «Обработка одномерной выборки»
Цель работы: закрепление теоретических сведений по способам представления, группировки и графической интерпретации эмпирических данных.
Краткие теоретические сведения
В результате наблюдений и регистрации массовых случайных явлений получаются эмпирические (статистические) данные или эмпирический материал. Если наблюдаемая величина является случайной, то ее можно изучать методами теории вероятностей. Для понимания характера поведения этой случайной величины нужно знать ее закон распределения.
Определение законов распределения рассматриваемых величин и оценка значений параметров распределения на основании наблюденных значений – основная задача курса «Эмпирические методы программной инженерии». Еще одной задачей курса является исследование методов обработки и анализа эмпирического материала с целью получения определенных выводов, необходимых для организации моделирования процессов с участием рассматриваемых величин.
Рассмотрим случайный эксперимент, связанный со случайной величиной 
. Осуществив 
независимых повторений этого эксперимента, мы получим последовательность наблюдений данных значений величины , которые обозначим 
. Эту совокупность значений называют выборкой, число ее элементов – объемом выборки, а числа 
- выборочными значениями.
Статистическая совокупность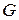 
называется генеральной, если исследованию подлежат все элементы совокупности. Чаще всего генеральная совокупность бесконечна, выборка есть конечная ее часть, доступная исследователю. Главное требование – независимость элементов выборки, что равносильно требованию случайности извлечения элементов.
Выборочный метод - статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов, взятых на выборку.
Для анализа и последующей обработки экспериментальных данных составляются вариационные ряды – последовательности наблюдаемых значений, записанных в возрастающем порядке. Наблюдаемые значения случайной величины X называются вариантами.
Пусть из генеральной совокупности извлечена выборка, причем варианта 
наблюдалась 
раз, 
– 
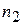раз, 
– 
раз и 
– объем выборки. Последовательность вариант, записанных в порядке возрастания, называют вариационным рядом. Количество наблюдений называют частотами, а их отношения к объему выборки 
– относительными частотами.
Пример 1. Объем потребления яблок в различных регионах Украины за месяц (тыс. ящиков): 100; 115; 80; 85; 95; 112; 125; 112; 112; 110; 130; 129; 80; 90; 95; 118; 120; 95; 110; 95; 95; 110; 128; 135.
Для примера 1 вариационный ряд имеет вид: 80, 80, 85, 90, 95, 95, 95, 95, 95, 100, 110, 110, 110, 112, 112, 112, 115, 118, 120, 125, 128, 129, 130, 135.
Частотным рядом называют перечень упорядоченных вариант и соответствующих им частот или относительных частот.
Для примера 1 частотный ряд имеет вид:
| |||||||||||||||
| |||||||||||||||
| 
| 
|
| 
|
| 
|
|
|
|
|
|
|
|
|
|
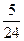
На практике большие выборки из распределений подвергаются группировке в виде интервального ряда. Интервальный статистический ряд для выборки строится следующим образом:
1) отыскиваются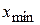 
и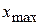 
(минимальная и максимальная варианты);
2) находится 
– амплитуда (размах) изменчивости выборки;
3) промежуток 
разбивается на 
интервалов, где - количество частичных интервалов, которое рекомендуется определить по формуле Стерджеса:
;
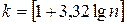4) шаг интервального ряда 
получают как отношение:
;
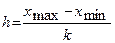5) для каждого частичного интервала находится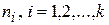 
, где 
– число вариант, попавших в i-й интервал;
6) составляется таблица:
| 
| … | 
|
| 
| … | 
|
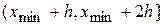
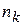
Для примера 1: 
, 
, 
, 
, 
. Тогда интервальный ряд имеет вид:
| [80, 91] | (91,102] | (102,113] | (113, 124] | (124, 135] | |
|
|
Примечание 1. Дискретный вариационный ряд получается из интервального, если за новые значения признака X взять середины интервалов.
Дискретный вариационный ряд для примера 1 имеет вид:
|
| 85,5 | 96,5 | 107,5 | 118,5 | 129,5 |
|
| |||||
|
| 
| 
|
| 
| 
|
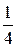
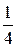
Для наглядности используют графические представления эмпирических значений.
Полигон частот – ломаная, отрезки которой соединяют точки 
, 
, …, 
. Для построения полигона частот на оси абсцисс откладывают варианты 
, а на оси ординат – соответствующие им частоты 
. Точки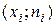 
соединяют отрезками прямых.
Для примера 1 полигон частот представлен на рис. 1.1.
Рисунок 1.1 - Полигон частот
Полигон относительных частот – ломаная, отрезки которой соединяют точки 
, 
, … .
Гистограмма частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты равны отношению 
(плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии .
Для примера 1 гистограмма частот представлена на рис. 1.2.
Рисунок 1.2 - Гистограмма частот
Площадь 
-го частичного прямоугольника равна 
– сумме частот вариант -го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т. е. объему выборки.
Гистограмма относительных частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты равны отношению 
(плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Площадь гистограммы относительных частот равна единице. Гистограмма является первым приближением плотности распределения количественного признака генеральной совокупности.
Пусть известно статистическое распределение частот количественного признака . Введем обозначения: 
– число наблюдений, при которых наблюдалось значение признака, меньшее 
; – общее число наблюдений (объем выборки). Ясно, что относительная частота события 
равна 
. Если будет изменяться, то будет изменяться и относительная частота, то есть относительная частота есть функция от . Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.
Таким образом, эмпирической функцией распределения (функцией распределения выборки) называют функцию 
, определяющую для каждого значения относительную частоту события. Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
По определению 
, где – число вариант, меньших , – объем выборки.
Для примера 1 эмпирическая функция распределения имеет вид:
Из определения функции вытекают следующие ее свойства:
1) значения эмпирической функции принадлежат отрезку [0,1]:
;
2) – неубывающая функция;
3) если 
– наименьшая варианта, то 
, при 
, если – наибольшая варианта, то 
при 
.
Контрольные вопросы
1. Что называется выборкой?
2. Дайте определение частотного ряда.
3. Как построить полигон частот?
4. Чем гистограмма частот отличается от полигона частот?
5. Дайте определение эмпирической функции распределения. Какими свойствами она обладает?
rt VLX, because it was unavailable, or its retrieval was aborted, or the project was stopped too soon. \n\nDo you want to open it from the server?'))window.location='http://studopedia.ru/pravo.php?n=8&id=138418'">Опубликованный материал нарушает авторские права?.