Методы оптимальных решений

В задаче определения условного экстремума уравнения ,х2, ……….х𝑛)= 0,1=1,2…., m,m<n называют: уравнение связи

Выбор наилучшего решения множества вариантов производства, распределения или потребления, осуществляется с помощью оптимизационных моделей

Венгерский метод применяется при решении задач целочисленного программирования

В транспортной задаче цикл в таблице с базисным распределением поставок, при котором одна из его вершин лежит в свободной клетке, остальные – в заполненных, называется циклом пересчета

Вследствие повышения цен на яблоки кривая спроса на груши сдвигается вправо

В транспортной задаче, где m – число поставщиков, n – число потребителей, количество переменных, подлежащих нахождению равно: m * n

В теории графов для любого дерева с m вершинами и n ребрами выполняется соответствие: m = n – 1

В транспортной задаче открытого типа имеется 3 поставщика и 5 потребителей некоторого однородного груза. Чтобы план перевозок не был вырожденным, число занятых клеток в таблице поставок должно быть равно: 8

В теории графов, связный без циклов называется: деревом

В задачах линейного программирования (при использовании геометрических построений) линия уровня : в направлении противоположном направлению вектора

В модели Солоу устойчивый рост объема выпуска расчете на одного занятого объясняется: технологическим прогрессом

В задачах линейного программирования вектор переменных Х, удовлетворяющий системе ограничений задачи, называют: допустимым.

В модели межотраслевого баланса основой информационного обеспечения является: технологическая матрица.

В статистических межотраслевых моделях не используются: межотраслевые потоки капитальных вложений

В схеме межотраслевого баланса количество квадрантов равно: 4

Вектор Х= ,х2, ………. )являющийся решением системы

и содержащий лишь неотрицательные компоненты, называется: допустимым

Вектор Х= ,х2, ………. )являющийся решением системы

называется допустимым, если для любых j=1,2, ……n выполняется:

В многоканальных системах массового обслуживания с неограниченной длиной очереди, очередь не растет бесконечно, если приведением интенсивность потока заявок p=λ/m удовлетворяет условие : p/n<1

В модели межотраслевого баланса матрица А является матрицей коэффициентов прямых материальных затрат

Величины конечной продукции в модели межотраслевого баланса Леонтьева находится по формуле: Y=(Е – А) Х

В модели международной торговли (линейной модели торговли) АХ – Х = 0, матрица А – это: структурная матрица торговли

 

Вектор Х= ,х2, ………. )являющийся решением системы

s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> и удовлетворяющую условие при котором линейная функция F= принимает максимальное или минимальное значение, называется: оптимальным решением

В одноканальной системе массового обслуживания с неограниченной очередью интенсивность потока заявок составляет 5 вызовов в минуту, а среднее время обслуживания одной заявки 10 секунд, среднее время пребывания заявки в системе равно: одна минута

В одноканальной системе массового обслуживания с неограниченной очередью интенсивность потока заявок составляет 5 вызовов в минуту, а среднее время обслуживания одной заявки 10 секунд. Среднее число заявок в очереди равно 4

В одноканальных системах массового обслуживания с неограниченной длиной очереди, очередь не растет бесконечно, если приведенная интенсивность потока заявок p=λ/m: p<1

Величины валовой продукции в модели межотраслевого баланса Леонтьева находятся по формуле: Х=(Е-А)

Для полуплоскости 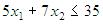точка А(3; 7) является внешней точкой.

 

Модель, соответствующая задаче нахождения переменных , удовлетворяющих системе неравенств (уравнений) ( ) где ( ),обращающих в максимум (или минимум) функцию 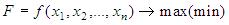, называется: задачей целочисленного программирования.

 

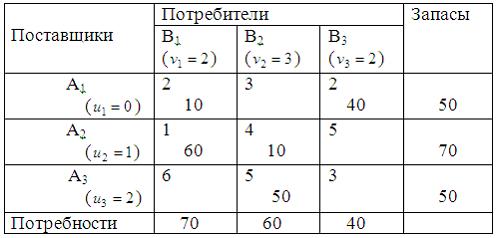
Для улучшения опорного плана транспортной задачи цикл пересчета следует построить для клетки: (3; 3).

 

Дана задача линейного программирования

Ограничения на искомые переменные двойственной задачи имеют вид:

Модели, которые используют такие наглядные элементы, как упругие шары, потоки жидкости, траектории движения тел, относятся к: образным.

Моделирование, в котором изучаются модели, предназначенные для воспроизведения динамики процессов, происходящих в изучаемом объекте, причем общность процессов основывается на сходстве их физической природы, называется физическим.

Модель задачи линейного программирования, в которой целевая функция исследуется на максимум и система ограничений задачи является системой уравнений, называется: канонической.

При решении задачи целочисленного программирования методом Гомори при необходимости вводится дополнительное ограничение . Вместо многоточия следует поставить знак

 

Методом целочисленного программирования требуется решать задачу о назначении

Выбор наилучшего решения из множества вариантов производства, распределения или потребления, осуществляется с помощью: оптимизационных моделей

Параллельными ребрами в графе называются ребра имеющие одинаковые концевые вершины

Если в транспортной задаче объем потребностей превышает объем запасов, в рассмотрение вводят: один фиктивный пункт производства.

Методом рекуррентных соотношений решается задача динамического программирования

Задача линейного программирования при условии максимизации целевой функции имеет оптимальное решение, если допустимое множество решений не пусто и ограничено сверху

Сетевой график задачи СПУ (сетевого планирования и управления) имеет четыре полных пути. Их длины: , , , .

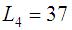Наибольшим полным резервом времени обладает второй путь.

Сетевой график задачи СПУ (сетевого планирования и управления) имеет четыре полных пути. Их длины: , , , .

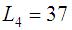Длина критического пути равна 41.

Уравнение Беллмана (рекуррентное соотношение) для задачи загрузки рюкзака имеет вид:

При анализе случайных процессов с дискретными состояниями удобно пользоваться графом состояний.

Рентабельной является продукция, для которой дополнительная двойственная переменная в оптимальном плане задачи:

Поиск разрешающего элемента в симплекс-таблице при решении задачи линейного программирования симплексным методом начинается с…

выбора разрешающего столбца.

 

Оптимальным в данной задаче линейного программирования является вектор X = (0; 4; 0)

Вероятность отказа в обслуживании заявок в многоканальной СМО равна 0,2. Приведенная интенсивность потока требований ( ) – 5. Среднее число занятых каналов равно 4.

Дана задача линейного программирования

Двойственной по отношению к данной является задача

Случайный процесс называется Марковским, если это: процесс без последствий.