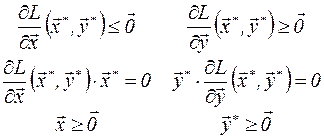Общая задача нелинейного программирования.

1. Рассмотрим задачу F(x) ® max, x ³ 0 (1)

В точке максимума либо 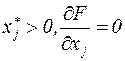, либо

Условие 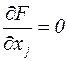при появлении ограничения x_j ³ 0заменяется

тройкой условий дополняющей нежесткости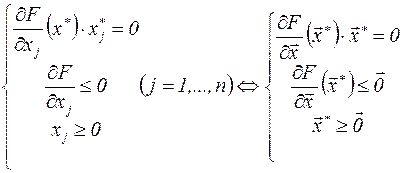

А что в точке минимума?

2. Рассмотрим задачу F(x) ® max, g(x) £ b, x ³ 0 (2)Добавим неотрицательные переменные

F(x) ® max, g(x) + s = b, x ³ 0, s³ 0

Без условий неотрицательности это классическая задача. Необходимое условие экстремума – равенство нулю всех частных производных функции Лагранжа L₀(x, s, y) = F(x) + y^.(b – g(x) – s) (их n + 2m)

При условиях неотрицательности x ³ 0,s ³ 0 равенства по x и s следует заменить тройками условий дополняющей нежесткости

 

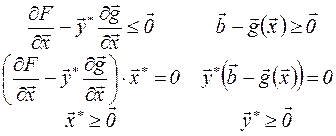
Это условия Куна-Такера локального максимума для общей задачи матем. программирования

 

3. Введем функцию Лагранжа для задачи (2). L(x,y) = F(x) + y^.(b – g(x))

Условия Куна-Такера Û