Уравнения Бернулли.

 

Определение 12. Уравнением Бернулли называется уравнение вида:

, (21)

где 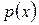, 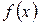– заданные функции; n – вещественное число, отличное от 0 и 1.

Для решения уравнения Бернулли следует обе его части разделить на и сделать подстановку 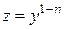. После подстановки получается линейное уравнение относительно z: 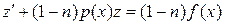, которое можно решить методом, изложенным в пункте 2.4. Однако применение метода решения из пункта 2.4. напрямую (без указанной подстановки) также позволяет успешно найти общий интеграл уравнения Бернулли.

Пример 7. Найти общее решение уравнения .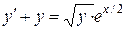

Решение. Подстановка приводит данное уравнение к виду 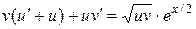. Решая уравнение , найдем его частное решение . Далее исходное уравнение преобразуется к виду 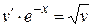, откуда , или 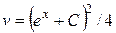. Таким образом, общее решение данного уравнения Бернулли есть .

 

Индивидуальные задания к параграфу 2.5.

Найти общий интеграл дифференциального уравнения.

1. ;

2. ;

3. ;

4. ;

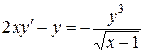5. ;

6. ;

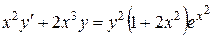7. ;

8. ;

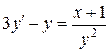9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. .