Логарифм произведения, частного от деления, степени и корня

Приведём сводку формул в предположении, что все значения положительны:

	Формула, Пример
Произведение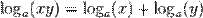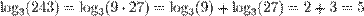
Частное от деления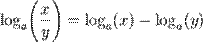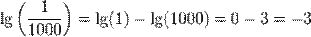
Степень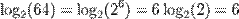
Корень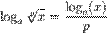

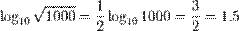
Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные значения переменных, например:

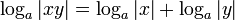
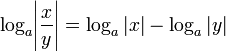
Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:

Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел с помощью логарифмических таблиц производилось по следующему алгоритму:

1. Найти в таблицах логарифмы чисел .

2. Сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения .

3. По логарифму произведения найти в таблицах само произведение.

Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично упрощались возведение в степень и извлечение корня.