Формулы Лапласа. Формула Пуассона
При больших значениях n использование формулы Бернулли связано с трудоёмкими вычислениями. Пусть нам нужно вычислить  :
:

Ясно, что это технически сложно. В подобных случаях используют формулу, являющуюся предельным случаем формулы Бернулли.
Локальная формула Лапласа. Если вероятность p появления события A постоянна в каждом испытании и отлична от 0 и 1, то вероятность  того, что событие A наступит k раз в n независимых испытаниях, при достаточно большом числе n приближенно равна
того, что событие A наступит k раз в n независимых испытаниях, при достаточно большом числе n приближенно равна
 , (2.3)
, (2.3)
где  – функция Гаусса (рисунок 2.2),
– функция Гаусса (рисунок 2.2),  .
.
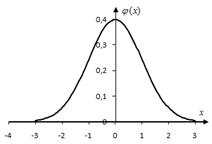
Рисунок 2.2
Чем больше n, тем точнее формула (2.3). При  она даёт удовлетворительные для практики результаты.
она даёт удовлетворительные для практики результаты.
Значения функции Гаусса  приведены в таблице Б.1 приложения Б.
приведены в таблице Б.1 приложения Б.
Свойства функции Гаусса:
1.  – четная функция, т.е.
– четная функция, т.е.  .
.
2. функция  монотонно убывает при положительных значениях x, причем при
монотонно убывает при положительных значениях x, причем при  (практически можно считать, что уже при
(практически можно считать, что уже при  ).
).
Пример 2.3. Вероятность изготовления детали высшего сорта на данном станке равна 0,4. Найти вероятность того, что среди наудачу взятых 56 деталей половина окажется высшего сорта.
Решение. n большое,  , поэтому применим локальную формулу Лапласа (2.3). Проведём необходимые вычисления:
, поэтому применим локальную формулу Лапласа (2.3). Проведём необходимые вычисления:
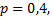



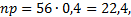



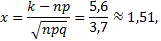

Следующая формула Лапласа позволяет находить вероятность  того, что событие A в n независимых испытаниях наступит не менее
того, что событие A в n независимых испытаниях наступит не менее 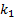 и не более
и не более  раз.
раз.
Интегральная формула Лапласа. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие A в n независимых испытаниях наступит не менее 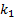 и не более
и не более  раз, при достаточно большом числе n приближенно равна
раз, при достаточно большом числе n приближенно равна
 (2.4)
(2.4)
 – функция Лапласа, (2.5)
– функция Лапласа, (2.5)
 (2.6)
(2.6)
При  формула (2.4) дает, как правило, удовлетворительную для практики погрешность вычисления вероятности.
формула (2.4) дает, как правило, удовлетворительную для практики погрешность вычисления вероятности.
Значения функции  можно найти в таблице Б.2 приложений. График
можно найти в таблице Б.2 приложений. График  изображён на рисунке 2.3. Перечислим свойства функции Лапласа.
изображён на рисунке 2.3. Перечислим свойства функции Лапласа.
1.Функция  нечетная, т. е.
нечетная, т. е.  .
.
2.Функция  монотонно возрастает, при
монотонно возрастает, при 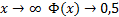 (практически можно считать, что уже при
(практически можно считать, что уже при  ).
).

Рисунок 2.3
Пример 2.4.В некоторой местности из каждых 100 семей 80 имеют холодильник. Какова вероятность, что от 300 до 360 семей включительно из 400 обследованных имеют холодильники?
Хорошо бы пример технический
Решение. Применим интегральную формулу Лапласа (  . Вначале определим по формулам (2.6)
. Вначале определим по формулам (2.6)
 .
.
Далее по формуле (2.4), учитывая свойства функции Φ(x), получим:
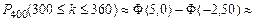
 .
.
(Из таблицы Б.2 приложения Б:  ).
).
Рассмотрим следствие интегральной формулы Лапласа.
Следствие. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе 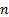 независимых испытаний вероятность следующих событий определяются по формулам:
независимых испытаний вероятность следующих событий определяются по формулам:
а) относительная частота  события A заключена в пределах от a до b:
события A заключена в пределах от a до b:
 (2.7)
(2.7)

б) относительная частота  события A отличается от его вероятности
события A отличается от его вероятности  не более, чем на величину
не более, чем на величину  (по абсолютной величине):
(по абсолютной величине):

При  и
и  формулы Лапласа дают удовлетворительную для практики погрешность вычисления вероятности. Если n одного порядка с 1/n при больших n, или
формулы Лапласа дают удовлетворительную для практики погрешность вычисления вероятности. Если n одного порядка с 1/n при больших n, или  , более точный результат дает формула Пуассона
, более точный результат дает формула Пуассона
 , (2.7)
, (2.7)
где  .
.
Пример 2.5. На факультете 730 студентов. Какова вероятность того, что 1 сентября является днём рождения одновременно трёх студентов?
Решение. Вероятность того, что день рождения для отдельного студента 1 сентября, равна p=1/365<0,1. Применяем формулу Пуассона (2.7). В нашем случае n=730, p=1/365, k=3, поэтому
 .
.
Таким образом, в среднем в 18 случаях из ста на 1 сентября приходится день рождения трёх студентов факультета.
2.1.Сколько нужно взять деталей, чтобы наивероятнейшее число годных деталей было равно 50, если вероятность того, что наудачу взятая деталь будет бракованной, равна 0,1?