Центральная предельная теорема
ЦПТ представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.
Теорема Ляпунова. Если 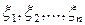 - независимые СВ, у каждой из которых существует математическое ожидание
- независимые СВ, у каждой из которых существует математическое ожидание  , дисперсия
, дисперсия  , абсолютный центральный момент третьего порядка
, абсолютный центральный момент третьего порядка  ,
, 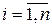 и
и  , то закон распределения суммы этих СВ
, то закон распределения суммы этих СВ  при
при  неограниченно приближается к нормальному с математическим ожиданием
неограниченно приближается к нормальному с математическим ожиданием  и дисперсией
и дисперсией  .
.
Сформулируем ЦПТ для случая, когда члены суммы имеют одинаковое распределение, поскольку он чаще других используется на практике.
Теорема. Пусть СВ 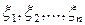 независимы, одинаково распределены, имеют конечные математическое ожидание
независимы, одинаково распределены, имеют конечные математическое ожидание  , дисперсию
, дисперсию  и абсолютные центральные моменты третьего порядка
и абсолютные центральные моменты третьего порядка  ,
, 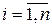 . Тогда функция распределения центрированной и нормированной суммы этих СВ стремится при
. Тогда функция распределения центрированной и нормированной суммы этих СВ стремится при  к функции распределения стандартной нормальной СВ:
к функции распределения стандартной нормальной СВ:
 ,
,
 .
.
Согласно этой теореме, при достаточно большом n  . Это означает, что сумма
. Это означает, что сумма  . Говорят, что при
. Говорят, что при  СВ
СВ  асимптотически нормальна.
асимптотически нормальна.
Проверим выполнение условия:
 .
.
Теорема позволяет при больших n вычислять вероятности различных событий, связанных с суммами СВ:
 .
.
Часто ЦПТ используется, если  .
.
Пример 3
Независимые СВ 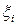 распределены равномерно на отрезке
распределены равномерно на отрезке  . Найти закон распределения СВ
. Найти закон распределения СВ  , а также вероятность того, что
, а также вероятность того, что  .
.
Условия ЦПТ соблюдаются, поэтому СВ 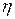 имеет приближенно плотность распределения
имеет приближенно плотность распределения
 .
.
Так как  ,
,  ,
,  , то
, то
 ;
;
 ;
;
 .
.
Тогда  .
.

Следствиями ЦПТ являются рассмотренные ранее локальная и интегральная теоремы Муавра-Лапласа. Приведем вывод интегральной теоремы Муавра-Лапласа.
Рассмотрим схему Бернулли. Пусть  - число появления события А в n независимых испытаниях, в каждом из которых оно может появиться с вероятностью p. СВ
- число появления события А в n независимых испытаниях, в каждом из которых оно может появиться с вероятностью p. СВ  , где
, где 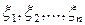 - независимые СВ такие что,
- независимые СВ такие что, 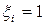 , если в i-ом испытании появилось событие А, и
, если в i-ом испытании появилось событие А, и 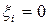 , если событии А не появилось.
, если событии А не появилось.
Так как СВ 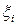 ,
, 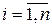 , независимы и одинаково распределены,
, независимы и одинаково распределены,  ,
,  , то согласно ЦПТ при большом n
, то согласно ЦПТ при большом n  .
.
Тогда  , где
, где  ,
,  . Получили интегральную теорему Муавра-Лапласа.
. Получили интегральную теорему Муавра-Лапласа.
Пример 4
Машинистке требуется напечатать текст, содержащий 8000 слов, состоящих из четырех и более букв. Вероятность сделать ошибку в любом из этих слов равна 0,01. Какова вероятность, что при печатании будет сделано не более 90 ошибок?
 .
.
Тогда  , где
, где  ,
,  . Получили интегральную теорему Муавра-Лапласа.
. Получили интегральную теорему Муавра-Лапласа.
Вероятность того, что событие А в n независимых испытаниях произойдет k раз можно приближенно вычислить по формуле:
 .
.
Чем меньше  , тем точнее приближенное равенство. Минимальное целое число
, тем точнее приближенное равенство. Минимальное целое число  .
.
Можно записать:
 ,
,
где  ,
,  .
.
При малом  имеем
имеем  , где
, где  - плотность распределения случайной величины
- плотность распределения случайной величины  , которая согласно ЦПТ имеет вид:
, которая согласно ЦПТ имеет вид:  .
.
Получаем локальную теорему Муавра-Лапласа:  , где
, где  - функция Гаусса,
- функция Гаусса,  .
.