Th2. Второй критерий
Для того, чтобы функциональная последовательность (1) равномерно сходилась к предельной функции  на множестве M необходимо и достаточно, чтобы
на множестве M необходимо и достаточно, чтобы
 (8)
(8)
□
Необходимость. Пусть выполняется условие (6), покажем, что тогда выполняется (8).
Возьмем  произвольное. По нему найдем N из выполнения условия (6).
произвольное. По нему найдем N из выполнения условия (6).
Если теперь  , то для всех
, то для всех 
 , тогда
, тогда  . В силу произвольности
. В силу произвольности 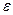 это означает выполнение (8).
это означает выполнение (8).
Достаточность. Пусть выполняется условие (8). Возьмем  - произвольное, тогда для этого
- произвольное, тогда для этого 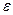 найдем N из выполнения условия (8): т.е. такое, что для
найдем N из выполнения условия (8): т.е. такое, что для  выполняется
выполняется  , тогда, тем более
, тогда, тем более  , то есть выполняется условие равномерной сходимости функциональной последовательности (6).
, то есть выполняется условие равномерной сходимости функциональной последовательности (6).
■
 I Исследуем функциональную последовательность на равномерную сходимость
I Исследуем функциональную последовательность на равномерную сходимость  ,
,  ,
,  .
.
1. Найдем предельную функцию  .
.
 , следовательно
, следовательно  .
.
2. Найдем  Исследуем на max, функцию
Исследуем на max, функцию  , производная
, производная 
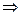

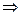
 - точка max,
- точка max,  ,
,  ,
,  - максимальное значение функции.
- максимальное значение функции.
3. Найдем  =
=

 =0.
=0.
Ответ: исходная функциональная последовательность сходится к  равномерно.
равномерно.