Th1. Критерий Коши равномерной сходимости функциональной последовательности
Для того, чтобы функциональная последовательность (1) равномерно сходилась на часловом множестве M необходимо и достаточно, чтобы
, такое, что при всех 
, 
и 
будет 
. (7)
□
Необходимость. Предположим, что функциональная последовательность сходится равномерно на множестве M. Обозначим 
- предельную функцию этой функциональной последовательности. Возьмем произвольное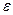 
и 
, для этого 
будет выполняться условие (6), тогда
.
Доказано (7).
Достаточность. Предположим, что числовое условие (7) выполняется в некоторой точке 
, тогда числовая последовательность 
сходится к предельной функции .
Докажем теперь равномерную сходимость.
Возьмем произвольно 
и положим . Обозначим через 
такое натуральное число, что при всех 
и и для будет выполняться (7). Так как 
и 
, тогда выполняется одновременно 
и 
.
Тогда
, что означает равномерную сходимость (1).
■