Задания для работы в аудитории
Задача №1. Изобразите при помощи кругов Эйлера отношения между множествами С и D, если:
а) С – множество двузначных чисел, D={3,43,34,56,103};
б) С – множество двузначных чисел, D – множество четных натуральных чисел;
в) С – множество двузначных чисел, D – множество трехзначных чисел;
г) С – множество двузначных чисел, D – множество натуральных чисел, не меньших 10.
Задача №2. Отношения между множествами всех выпуклых четырехугольников (А), параллелограммов (В), прямоугольников (С), ромбов (Д) и квадратов (Е) изображены на рисунке. Покажите каждое из множеств.

Задача №3. Найдите пересечение множеств:
а) А={a, b, c, d, e, f,}, B={b, d, e, g, h};
б) А={х: –  £ х £
£ х £ 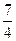 }, В={х: –
}, В={х: –  £ х £ 2}.
£ х £ 2}.
Задача №4. Известно, что х ÎА. Следует ли из этого, что хÎА Ç В?
Задача №5. Известно, что хÎА Ç В. Следует ли из этого, что хÎА?
Задача № 6. Из каких элементов состоит пересечение множества букв в слове «МАТЕМАТИКА» и множества букв в слове «ГЕОМЕТРИЯ»?
Задача № 7. М – множество однозначных чисел, Р – множество нечетных натуральных чисел. Из каких чисел состоит пересечение данных множеств? Содержатся ли в нем числа –7 и 9?
Задача № 8. А – множество точек окружности, В – множество точек прямой l. Из скольких элементов может состоять пересечение данных множеств? Может ли оно быть пустым?
Задача № 9. М – множество спортсменов в некоторой школе, Р – множество мальчиков в этой школе. Изобразите эти множества при помощи кругов Эйлера. Укажите характеристическое свойство элементов множества МÇР.