Закон эксцентриситета (закон Релея)
Закону распределения эксцентриситета подчиняются величины, которые могут принимать только положительные значения, например, эксцентриситет, биение, разностенность, бочкообразность, непараллельность, овальность и т.д. Закон Релея формируется, в частности, тогда, когда случайная величина представляет собой геометрическую сумму двух случайных величин
 ,
,
каждая из которых подчиняется закону нормального распределения с параметрами:
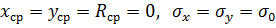 .
.
 Уравнения кривой, характеризующий закон Релея (рис. 5) имеет вид:
Уравнения кривой, характеризующий закон Релея (рис. 5) имеет вид:
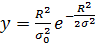 ,
,
где  – среднее квадратическое отклонение значений координат x и y конца радиус-вектора R.
– среднее квадратическое отклонение значений координат x и y конца радиус-вектора R.
Анализ уравнения кривой закона Релея показывает, что при  , а при
, а при  , т.е. начало кривой распределения совпадает с началом координат, а нисходящая ветвь асимптотически приближается к оси абсцисс (рис. 5).
, т.е. начало кривой распределения совпадает с началом координат, а нисходящая ветвь асимптотически приближается к оси абсцисс (рис. 5).
Основные параметры закона Релея:
 ,
,  1,253
1,253 
Фактическое поле рассеивания значений переменной величины радиус-вектора R находят из выражений:
5,252 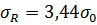 .
.