Кут між векторами. Умова колінеарності і перпендикулярності векторів.

 

Кутом 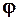між двома ненульовими векторами називають найменший кут, на який потрібно повернути один з векторів, щоб його напрям співпав з напрямом другого. Позначається .

 

Скалярним добутком векторів і називається число, рівне добутку довжин цих векторів на косинус кута між ними

.

По відомим координатам векторів легко знайти кут між ними із співвідношення

Приклад 1.1 Знайти кут між векторами і .

Розв’язок. Знайдемо довжини векторів:

Тоді

.

.

Зауважимо, що у випадку , то

.

Необхідною і достатньою умовою колінеарності двох ненульових векторів і є рівність . Якщо вектори і задані в координатній формі: , , то умова колінеарності запишеться наступним чином:

.

Тобто, необхідною і достатньою умовою колінеарності векторів є пропорційність їх одноімених координат.

Необхідною і достатньою умовою перпендикулярності векторів і є рівність , або в координатній формі:

.

Приклад 1.2. При яких значеннях параметра m вектори і колінеарні (перпендикулярні)?

Розв’язок. З умови колінеарності випливає, що

.

А з умови перпендикулярності

.