Геометрический смысл смешанного произведения

Построим параллелепипед на векторах 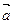, , 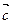с общим началом, как на ребрах. Пусть вектор

 

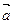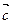
Тогда = , где для правой тройки векторов , , , для левой, наоборот, .

Таким образом, = , (8.17)

где V – объем параллелепипеда, образованного векторами , , .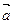

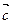Смешанное произведение векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

Отсюда,

, (8.18)

, (8.19)

 

. (8.20)