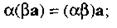Линейные операции над векторами

Линейными операциями над векторами называются сложение, вычитание и умножение вектора на число.

Суммой двух векторов a и b называется третий вектор с, начало которого совпадает с началом вектора а, а конец - с концом вектора b при условии, что вектор b отложен из конца вектора а. Вектор с получается по правилу треугольника или по правилу параллелограмма (рис 1)

Аналогично определяется сумма трех и более векторов. Суммой п векторов a1, a2, …, , называется вектор, начало которого совпадает с началом первого вектора, а конец - с концом последнего , при условии, что каждый последующий вектор отложен из конца предыдущего. Указанный способ построения суммы называется правилом замыкающей.

Очевидно, сумма векторов обладает свойством переместительности (коммутативности)

и свойством сочетательности (ассоциативности)

При определении суммы не предполагалось, что векторы являются компланарными. Сумма трех некомпланарных векторов а, b, с, наряду с правилом замыкающей, получается и по правилу параллелепипеда: сумма а+b+с равна вектору d , где d - диагональ параллелепипеда, построенного на векторах а, b, с, отложенных из одной точки О (рис.).

Из определения суммы следует, что

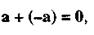Разностью а - b двух векторов а и b называется такой вектор d, который в сумме с вектором b дает вектор а:

Чтобы получить разность а - b двух векторов а и b, необходимо отложить их из одной точки и соединить конец второго вектора с концом первого (рис.).

Отметим, что

Произведением вектора а на число 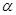называется новый вектор

удовлетворяющий условиям:

1) |b| = |а|;

2) а и b одинаково направлены при > 0;

3) а и b имеют противоположные направления при 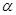< 0

Произведение вектора на число обладает следующими свойствами: