Линейная зависимость векторов

 

Пусть дана система п-мерных векторов .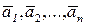

Опр. Линейной комбинацией векторов 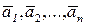называется вектор, равный сумме произведений этих векторов на произвольные действительные числа:

= ,

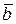где - некоторые коэффициенты.

Пример. Составить линейную комбинацию векторов

Опр. Говорят, что вектор 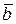разлагается по системе векторов 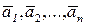, если вектор 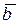можно представить в виде линейной комбинации векторов :

.

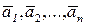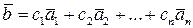Опр. Выпуклой линейной комбинацией векторов 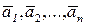называют линейную комбинацию,в которой все коэффициенты неотрицательны, и сумма коэффициентов равна единице.

 

Опр. Векторы 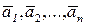называют линейно независимыми, если их линейная комбинация равна нулю только при нулевых значениях коэффициентов:

.

В противном случае векторы называют линейно зависимыми. Т.е. векторы линейно зависимы, если при выполнении равенства

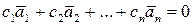
среди чисел найдется хотя бы одно ненулевое.

Пример. Доказать, что векторы и из предыдущего примера линейно независимы.

 

Теорема. Система векторов 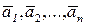является линейно зависимой, если хотя бы один из векторов этой системы можно представить в виде линейной комбинации остальных векторов системы. Верно и обратное утверждение.

Док-во. Пусть линейная комбинация векторов равна нулю, и при этом среди коэффициентов есть ненулевой, например,

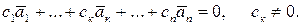
Тогда 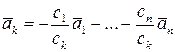, т.е.один из векторов системы представлен в виде линейной комбинации других.

Пусть теперь один из векторов равен линейной комбинации других, т.е.

.

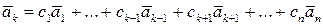(перенесем все в одну часть)

.

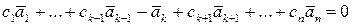Линейная комбинация равна нулю, и при этом не все коэффициенты нулевые, т.е. система линейно зависима.▲

 

Нетрудно доказать, что различные п-мерные единичные векторы линейно независимы.

Самостоятельно.

 

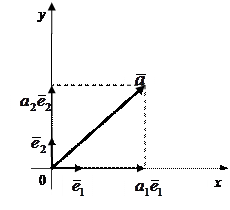Каждый п-мерный вектор 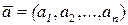может быть представлен единственным образом в виде линейной комбинации единичных п-мерных векторов с коэффициентами, равными координатам вектора

.