МЕТОД КООРДИНАТ.

26.Вершины треугольника имеют координаты А(1;6), В(- 4; 3), С(-2;-5). Найдите длину медианы AМ треугольника ABC.

Решение: Определим координаты середины отрезка ВС: М(-3; -1). Найдем расстояние между точками А и М, т. е. длину медианы AM. AM = = .

27.Найдите геометрическое место точек плоскости xy, для которых |x| = 5. Ответ: две прямые х=±5.

28.Найдите на оси абсцисс точку, равноудаленную от точек (1; 2) и (2; 3).

Решение: Пусть на оси Ох лежит точка С(х,0) Тогда должно выполнятся равенство СА=СВ, т.е. СА= , СВ= . (х-1)²+4=(х-2)²+9. Отсюда х=4, С(4,0).

 

29.Вершины треугольника имеют координаты А(1;6), В(4;3), С(0; 5). Найдите длину биссектрисы АК треугольника ABC.

Решение: По формуле деления отрезка в данном отношении найдем координаты точки К. Так как ВК:КС = АВ:АС, то вычислим предварительно АВ и АС.

AB= , АС = . Точка К имеет координаты (1; ). Тогда вектор АК имеет координаты АК(0, - ). Найдем расстояние АК, т. е. длину биссектрисы АК= . Ответ:1,5.

30.Даны точки А(2; 0) и В(-2; 6). Напишите уравнение окружности, диаметром которой является отрезок АВ.

Решение: Общий вид уравнения окружности: (x-x₀)²+(y-y₀)²=R². AB= , R= . x₀=0, y₀=3. Тогда (x-0)²+(y-3)²=13. x²+(y-3)²=13.

31.Найдите координаты центра окружности, лежащего на оси абсцисс, если известно, что окружность проходит через точку (1; 4) и радиус окружности равен 5.

Решение: Найти: (x₀, y₀). y₀=0. Уравнение окружности: (x-х₀)²+y²=25. Т.к. (1,4) лежит на окружности, то координаты удовлетворяют уравнению окружности: (1-х₀)²+4²=25. Отсюда x₀=4, x₀=-2. Тогда (x₀, y₀)=(4,0) или (x₀, y₀)=(-2,0).

32.Составьте уравнение геометрического места точек, равноудаленных от двух данных точек А(0; 1) и В(1; 2).

Решение: Пусть М(х,у) точка принадлежащая искомой кривой. По условию должно выполнятся равенство МА=МВ. Т.е. МА²=(х-0) ²+(у-1)², МВ²=(х-1) ²+(у-2)², или

х ²+(у-1)²= (х-1) ²+(у-2)², после преобразований получим 2у-2х-3=0 или – уравнение прямой.

33.Составьте уравнение прямой, которая проходит через точки А(-1; 1) и В(1; 0).

Решение: Общий вид уравнения прямой y=kx+b. Т.к. точки А и В принадлежат этой прямой, то можно подставить координаты точек в уравнение. Тогда найдем, что b=-1, k=-2. y=-2x-1.

34.Докажите, что прямые x + 2y = 3 и 2x + 4y = 3 не пересекаются.

Решение: после преобразований получим, что k₁=k₂.

35. Найдите наибольшее и наименьшее значение выражения , если .

Решение: Легко показать, что графиком уравнения 2|х|+|у|=2 является ромб ABCD. Тогда условие можно переформулировать так: найти наименьшее и наибольшее значение суммы длин отрезков МО и МК, где О(0; 0), К(0;-3), аточка М(х; у) принадлежит ромбу ABCD. Рассмотрим треугольник МОК. Имеем МО + МК≥ОК = 3 (равенство достигается, если точка М совпадает с точкой С). Далее: МО≤АО и МК≤АК. Складывая два последних неравенства, получаем МО + МК ≤ АО + АК = 7 (равенство достигается, если точки М и А совпадают).

Ответ:наибольшее значение выражения равно 7, наименьшее значение равно 3.

36.При каком значении с прямая x + y + c = 0 касается окружности x² + y² = 1?

Решение: Общую точку находим, решая систему: Выражаем х=-у-с, подставляем во 2-е уравнение, получим у²+2ус+с²+у²-1=0, Решаем квадратное уравнение относительно у, получим, D/4= 2-с². Т.к. точка одна, то нужно 1 решение, т.е. D/4=0 или с²=2, с= . Ответ: .

37.Решите систему уравнений:

Решение: Рассмотрим в прямоугольной системе координат хОу точки А(х; у), В(1; 0), С(-1; 0). Тогда по формуле расстояния между двумя точками имеем: АВ= , АС= . Тогда первое уравнение системы примет вид |АВ|+|АС|=2, это урав­нение отрезка ВС. Преобразуем второе уравнение системы х²-4х+4+у²=4 или

(х-2)²+у²=2², это есть уравнение окружности с центром в точке (2; 0) ради­усом 2. Ясно, что решением системы являются координаты - точки пересечения окружности и отрезка, т. е. пара чисел (0; 0).

38.При каком значении параметра а модуль разности корней уравнения х² - 6х + 12 + а² = 4а принимает наибольшее значение?

Решение: Переписав данное в условии уравнение в виде

(х-З)²+(а-2)²-1, построим его график в системе координат хОа. Очевидно, модуль разности корней уравнения примет наибольшее зна­чение в том случае, когда точки пересечения окружности с прямой, параллельной оси абсцисс, будут наиболее друг от друга удалены. По­нятно, что эта прямая должна проходить через центр окружности, а зна­чит, значение а равно двум.

Ответ:а = 2.

39.Докажите, что при любых x, y, z выполняется неравенство .

Решение: На координатной плоскости рассмотрим точки: А(х,0) В( , ), С( , ). Тогда АВ= , АС= , ВС= . По неравенству треугольника будем иметь АВ+ВС≥АС, что и требовалось доказать.

40.Найдите наименьшее значение выражения .

Решение: На координатной плоскости хОу рассмотрим точки А(1; 0), В(0; 1) и не­которую точку М(х; у). Тогда, сумма отрезков MB и МА, равная , будет наименьшей в том случае, когда точка М принадлежит отрезку АВ, т. е. MA + MB = AB= . Подчерк­нем, что наименьшее значение данного выражения достигается в любой точке отрезка АВ. Ответ: .

41.Решите систему уравнений:

Решение: Как и в предыдущей задаче, на координатной плоскости рассмотрим точки А(2;4), В(5;8) и М(х; у). Тогда неравенство треугольника MA+MB≥АВ в координатной форме выглядит так: ≥ 5. Ясно, что равенство возмож но лишь в том случае, когда точка М(х;у) принадлежит отрезку АВ. Уравнение прямой АВ имеет вид

Ах-bу + 4 = 0. Получаем систему, равносильную исходной:

4х-Зу+4 = 0, Зху-10у=3, 2≤х≤5. Ее решение х=3,5; у=6. Ответ:х = 3,5; у =6.

42.Напишите уравнение всех прямых, отсекающих от окружности хорду длины 6.

Решение: (указание: расстояние от (0,0) до прямых, отсекающих хорду, постоянно). Пусть расстояние от начала координат до прямой у=кх+b, отсекающей от окружности хорду длиной 6, равно h. Рассмотрим ∆ОВС 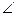OBC=90°. ОС = 5; BC= 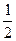AC=3, (по теореме о хорде: перпендикуляр опущенный на хорду делит ее пополам). OB=h=4 (∆ОВС - египетский); 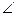BOD=а OD=b, h=bcosa; cosa= , , 4= , ; -уравнение прямых, отсекающих хорду длиной 6.

43.Найдите геометрическое место точек, сумма квадратов расстояний от которых до вершин равностороннего треугольника равна квадрату периметра этого треугольника.

Решение:Построим равносторонний треугольник со стороной а. Так чтобы начало координат совпало с центром треугольника, а одна из сторон была параллельна оси Ох. Тогда получим координаты вершин треугольника: А( , ), В(0, ), С( , ). Сумма квадратов расстояний от точки М(х,у)до вершин треугольника равна: АМ²+МВ²+МС²=Р², Р²=(3а)². Так как - расстояние между двумя точками с координатами (x₁,y₁) и (х₂,у₂), то АМ²=(х+ )²+(у+ )², МВ²=х²+(у- )², МС²=(х- )²+(у+ )².

Тогда

(х+ )²+(у+ )²+ х²+(у- )²=(х- )²+(у+ )²=(3а)². После преобразований, получим 3x²+3y²+a²=9a². x²+y²= a². т.е. искомое геометрическое место точек - это окружность с центром (0,0) и радиусом , а- сторона треугольника.

return false">ссылка скрыта

 

44.Найдите площадь треугольника с вершинами А(1;4), В(-3; -1), С(2; -2).

Решение: Воспользуемся формулой Герона, для этого найдем все стороны треугольника: АВ=с= , АС=b= ,

ВС=а= . S= =(подставив все данные, и преобразовав, получим)=14,5.

45.Докажите, что сумма квадратов расстояний от любой точки окружности, описанной около правильного треугольника, до трех вершин постоянна и равна удвоенному квадрату стороны этого треугольника.

Решение: Введем систему координат хОу, так чтобы цент треугольника совпал с началом координат, а одна сторона была параллельна оси ОХ. Отметим координаты вершин треугольника. А( , ), В(0, ), С( , ). Так как радиус окружности R= иее центр лежит в начале координат, то уравнение окружности примет вид: x²+y²= a². x²= - y².

Сумма квадратов расстояний от точки М(х,у) принадлежащей окружности, до вершин треугольника равна: АМ²+МВ²+МС²=2а².

АМ²=(х+ )²+(у+ )², МВ²=х²+(у )², МС²=(х- )²+(у+ )². Тогда

(х+ )²+(у+ )²+ х²+(у- )²=(х- )²+(у+ )²=2а². После преобразований, получим 2а²=2a². Что и требовалось доказать.

46.Найдите расстояние от центра окружности радиуса 9 см до точки пересечения двух взаимно перпендикулярных хорд длиной 16 см и 14 см соответственно.

Решение: Проведем ОЕ АС, OF BD. Из ∆ОАЕ: АЕ= 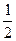АС=8. По теореме Пифагора, ОЕ= . Из ∆ODF, DF= 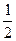DB=7, OF= . Из ∆ONE, NE=OF= ,

ON= = 7.