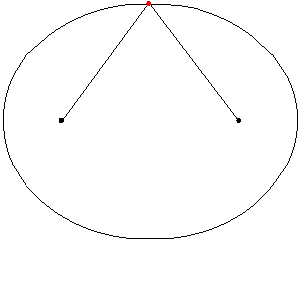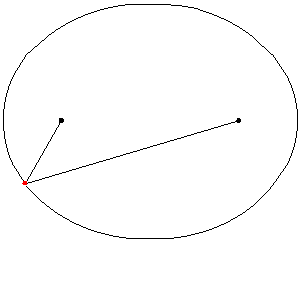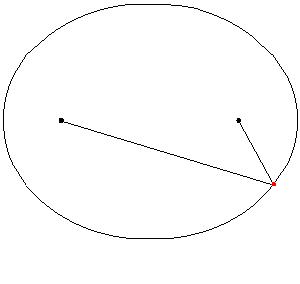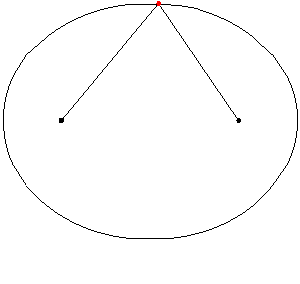
Соотношение между элементами эллипса

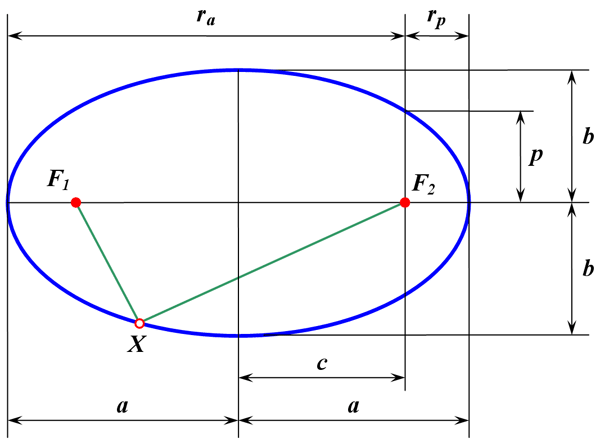
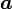  • — большая полуось;
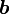  • — малая полуось;
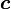  • — фокальный радиус (полурасстояние между фокусами);
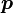  • — фокальный параметр;
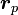  • — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
  • — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе).

Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек F1 и F2 (фокусов) есть постоянная величина 2a, причем 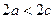, где 2c – расстояние между фокусами.

Каноническое уравнение гиперболы:

,

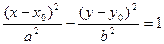где .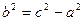

Параметр a называется вещественной полуосью гиперболы и представляет собой расстояние от начала координат до вершины гиперболы, параметр b называется мнимой полуосью.

Параметр c= есть расстояние от фокуса до начала координат.

Отношение 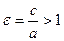называется эксцентриситетом гиперболы.

Расстояние от любой точки гиперболы М(x, y) до ее фокусов (фокальные радиусы) находятся по формулам

, .

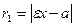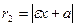Прямые, заданные уравнениями 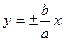, называются асимптотами гиперболы.

 

 

Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).

Каноническое уравнение параболы

.

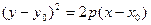Прямая 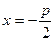- директриса параболы.

Частные случаи:

1) y2 = 2рx - парабола симметрична относительно оси Оx.

2) x2 = 2рy - парабола симметрична относительно оси Оy.

Фокальный радиус точки М(x, y) находится по формуле .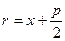

Парабола, ось которой параллельна оси OY, описывается уравнением

.
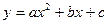