Тема 10. Прямая и плоскость в пространстве
1. Уравнение плоскости:
· перпендикулярной данному вектору  и проходящей через данную точку
и проходящей через данную точку 
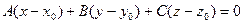 ;
;
· в отрезках

(a, b, c – отрезки, отсекаемые соответственно на осях Ox, Oy, Oz);
· общее
Ax+By+Cz+D=0.
2. Расстояние d от точки  до плоскости Ax+By+Cz+D=0 находится по формуле:
до плоскости Ax+By+Cz+D=0 находится по формуле:
 .
.
3. Даны две плоскости  и
и  .
.
Угол φ, образованный двумя плоскостями находится из соотношения:
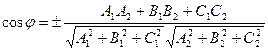 .
.
Условие параллельности двух плоскостей:
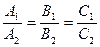 .
.
Условие перпендикулярности двух плоскостей:
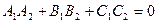 .
.
4. Уравнение прямой в пространстве:
· как линии пересечения двух плоскостей:

· проходящей через данную точку 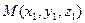 с направляющим вектором
с направляющим вектором  :
:
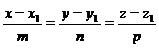
(канонические уравнения прямой);

(параметрические уравнения прямой);
· проходящих через две данные точки  и
и 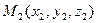 :
:
 .
.
5. Даны две прямые с направляющими векторами  и
и  .
.
Угол φ, между двумя прямыми находится из соотношения:
 .
.
Условие параллельности двух прямых в пространстве:
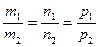 .
.
Условие перпендикулярности двух прямых в пространстве:
 .
.
6. Дана прямая  и плоскость Ax+By+Cz+D=0.
и плоскость Ax+By+Cz+D=0.
Угол φ, между прямой и плоскостью определяется из соотношения:
 .
.
Условие параллельности прямой и плоскости:
 .
.
Условие перпендикулярности прямой и плоскости:
 .
.