Синхронный ЭД, как объект управления. Динамические модели синхронного ЭД и синхронный ЭП в переменных «входы-выходы»

Математическое описание синхронной машины, необходимое для создания простой и удобной динамической модели должно включать в себя:

- уравнение зависимости синхронного момента синхронной машины от нагрузки;

- уравнение зависимости асинхронного момента синхронной машины от динамической жесткости.

Математическая модель синхронного ЭП, кроме перечисленных двух уравнений, должна содержать также классическое уравнение движения ЭП:

, (73)

где 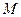- момент, созданный 3-х фазной обмоткой статора.

Если иметь в виду, что область номинальных нагрузок (моментов) соответствует углу рассогласования , находящемуся в пределе , и в этой области зависимости носит практически линейный характер, то:

(74)

Известно, что может быть физически представлен в виде жесткости упругой электромагнитной связи, которая в этом случае будет аналогична жесткости упругой связи в механической модели ЭП (см. главу «Динамические модели 2-х массовой механической системы»). При этом растяжение упругой электромагнитной связи между осями в магнитном поле и ротора, равное углу , будет зависеть от скорости, с которой вращается магнитное поле статора, и от скорости, с которой стремится вращаться ротор. Если при этих условиях продифференцировать уравнение (74), то получим:

(75)

Кроме того, известно, что ротор синхронной машины снабжён дополнительной обмоткой типа «беличье колесо», которая обеспечивает дополнительную составляющую момента (асинхронную), которую можно представить как:

, (76)