Определение необходимой численности выборки

Средняя квадратическая (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности. Уменьшение стандартной ошибки выборки, а следовательно, увеличение точности оценки, всегда связано с увеличением объема выборки. В этой связи уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений. Предельная ошибка выборки, вероятность ее появления и вариация признака предварительно известны. Приведем наиболее часто применяемые на практике выражения необходимого объема выборки:

 

n случайная и механическая выборка:

(повторный отбор)

(бесповторный отбор)

n типическая выборка

(повторный отбор)

(бесповторный отбор)

n серийная выборка

(повторный отбор)

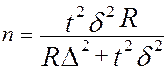(бесповторный отбор)

Величина 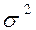характеризующая дисперсию признака в генеральной совокупности, зачастую бывает неизвестна. Поэтому используют приближенные способы оценки генеральной дисперсии.

1. Можно провести «пробное» обследование (обычно небольшого объема), на базе которого определяется величина дисперсии признака, используемая в качестве оценки генеральной дисперсии.

2. Можно использовать данные прошлых выборочных обследований, проводившихся в аналогичных целях, т.е. дисперсия, полученная по их результатам используется в качестве оценки генеральной дисперсии.

3. Если распределение признака в генеральной совокупности может быть отнесено к нормальному закону распределения, то размах вариации примерно равен откуда .

При проведении социально-экономических исследований, как правило, можно с достаточной точностью указать максимально и минимально возможные значения признака в исследуемой совокупности.

При определении по материалам выборки доли признака, а не средней его величины, объем выборочной совокупности при случайном отборе определяется по формулам:

(повторный отбор)

(бесповторный отбор)

При других видах отбора легко получаются аналогичные формулы. Если частость даже приблизительно не известна, то дисперсию доли полагают равной максимальному значению .