системы линейных неравенств с двумя переменными
Рассмотрим систему т линейных неравенств с двумя переменными вида
 (2.1)
(2.1)
и  . (2.2)
. (2.2)
Как известно, множеством решений каждого такого неравенства является полуплоскость вместе с ее границей (прямой), т. е. выпуклое множество без угловых точек, или иначе — выпуклый многоугольник.
Возьмем систему, состоящую из двух первых неравенств данной системы. Множеством ее решений (если она совместна) служат точки, которые принадлежат полуплоскостям решений обоих неравенств, т. е. принадлежат их пересечению. Согласно свойству выпуклых множеств (см. теорему §1), это множество является выпуклым и имеет конечное число угловых точек. Таким образом, множеством решений совместной системы двух линейных неравенств с двумя переменными служит выпуклый многоугольник. Присоединяя к двум неравенствам третье, аналогично установим, что решением системы трех линейных неравенств является выпуклый многоугольник, и т. д. Применяя метод математической индукции, аналогично устанавливаем, что множеством решений системы т линейных неравенств с двумя переменными является выпуклый многоугольник (исключая случай, когда система несовместна).
Если рассматривать множество решений линейных неравенств с п переменными, а затем систем таких неравенств, то в результате можно доказать, что множеством решений системы-т линейных неравенств с п переменными является выпуклый многогранник в п-мерном пространстве (исключая случай, когда система несовместна).
Пример 1. Построить множество решений системы линейных неравенств и найти координаты угловых точек этого множества

Ответ: Многоугольник с вершинами в точках 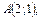
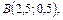
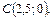
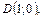

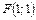 .
.