Постановка задачи линейного программирования

Найти максимум функции

при ограничениях:

Такая форма задачи линейного программирования называется канонической формой.

Не ограничивая общности, можем считать, что все числа 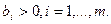Этого можно добиться, умножая ограничения, где на -1.

Множество допустимых решений задачи

X = { }

есть выпуклое множество, которое геометрически представляет собой выпуклый многогранник, имеющий конечное число крайних точек.

Крайней точкой выпуклого множества X называется точка X, которая не может быть выражена в виде выпуклой комбинации других точек X, .

Множество крайних точек многогранника X соответствует множеству допус­тимых базисных решений системы, и при этом одному базисному решению соот­ветствует одна крайняя точка многогранника.

Если функция в задаче линейного программирования достигает максимума на многограннике X, определяемом ограничениями, то она достигает его по край­ней мере в одной крайней точке этого многогранника. Если она достигает его в не­скольких крайних точках, то она достигает его на любой выпуклой комбинации этих крайних точек. Это утверждение определяет стратегию решения задачи, реализованную с помощью симплекс-метода, т. е. направленный перебор базисных решений, определяющих крайние точки многогранника. Направленность перебо­ра предполагает следующую организацию вычислительного процесса.

1. Определение начального базисного решения.

2. Переход от одного базисного решения к другому таким образом, чтобы обеспе­чить возрастание целевой функции .

2.2. Задача безусловной оптимизации

Общая постановка задачи безусловной оптимизации представляется следующим образом.

Дана дважды непрерывно дифференцируемая функция , определенная на множестве . Требуется исследовать функцию на экстремум, т. е. определить точки ее локальных минимумов и максимумов.

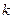Подавляющее большинство численных методов оптимизации относится к классу итерационных, т. е. порождающих последовательность точек в соответс­твии с предписанным набором правил, включающим критерий окончания. При заданной начальной точке методы генерируют последовательность Преобразование точки в представляет собой -ую итерацию.

Для определенности рассмотрим задачу поиска безусловного локального ми­нимума:

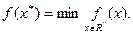
Численное решение этой задачи, как правило, связано с построением последо­вательности { } точек, обладающих свойством убывания целевой функции:

Общее правило построения последовательности { }имеет вид где точка - начальная точка поиска; - приемлемое направление перехода из точки в точку обеспечивающее выполнение свойства убывания целевой функции и называемое направлением спуска; 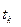- величина шага.

Начальная точка поиска задается исходя из физического содержания решае­мой задачи и наличия априорной информации о положении точек экстремума.

Приемлемое направление спуска должно удовлетворять условию = 0, 1,...,

где - градиент непрерывно-дифференцируемой функции в точке , обес­печивающему убывание целевой функции . Примером приемлемого направле­ния спуска является направление вектора антиградиента: .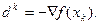

Величина шага выбирается либо из свойства убывания целевой функции, либо из условия минимума целевой функции вдоль направления спуска: