Выборочные МО, дисперсия, ковариация и корреляция. Связь истинных и выборочных значений.
Выборочное математическое ожидание показывает среднее значение выборки.
Для вычисления математического ожидания, нужно:
- Просуммировать все значения выборки.
- Полученное поделить на ее объем.
Формула:
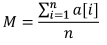
Выборочная дисперсия показывает насколько значения выборки отдалены от ее математического ожидания. Чем значение больше, тем данные более разбросаны.
Для вычисления дисперсии, нужно:
- Вычислить математическое ожидание выборки.
- От каждого элемента выборки вычесть мат. ожидание и возвести разность в квадрат.
- Просуммировать все полученные выше значения.
- Поделить сумму на объем выборки минус 1.
Формула:
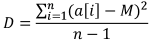
Выборочная ковариация - это величина, показывающая степень линейной зависимости между двумя выборками данных. Между линейно независимыми данными ковариация будет равняться 0.
Для вычисления ковариации двух выборок, нужно:
- Вычислить математическое ожидание первой выборки.
- Вычислить математическое ожидание второй выборки.
- Просуммировать все произведения двух разностей: первая - элемент первой выборки минус мат. ожидание первой выборки; вторая - элемент второй выборки (соответствующий элементу первой выборки) минус мат. ожидание второй выборки.
- Полученное поделить на объем выборки минус 1.
Формула:
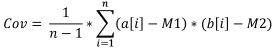
Выборочная коррелляция так же показывает степень линейной зависимости между двумя выборками, но ее значение всегда колеблется от -1 до 1.
Для вычисления корреляции двух выборок, нужно:
- Вычислить дисперсию первой выборки.
- Вычислить дисперсию второй выборки.
- Вычислить ковариацию этих выборок.
- Ковариацию поделить на корень из произведения дисперсий.
Формула:
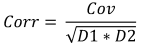
(В ЭТОМ НЕ УВЕРЕН)Для проведения статистического анализа данных, основанного на этой выборочной характеристике, необходимо знать ее статистические свойства. Это позволит судить о точности приближения к истинному значению 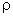 , строить статистические критерии для проверки различных гипотез о численных значениях анализируемого коэффициента корреляции, конструировать доверительные интервалы для истинного значения коэффициента корреляции. В классической математической статистике известны приближенные выражения для распределения
, строить статистические критерии для проверки различных гипотез о численных значениях анализируемого коэффициента корреляции, конструировать доверительные интервалы для истинного значения коэффициента корреляции. В классической математической статистике известны приближенные выражения для распределения 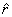 в случае
в случае  , а также для распределения величины (В ЭТОМ НЕ УВЕРЕН)
, а также для распределения величины (В ЭТОМ НЕ УВЕРЕН)