Анализ собранных материалов

Радость видеть и понимать есть самый прекрасный дар природы.

А. Эйнштейн

Анализ материалов наблюдений, опроса, анкетирования и т.п. начинается с их классификации. Эту работу можно выполнить еще до окончания диагностики или наблюдений, установив критерии их упорядоченности и фиксации. Группировка может осуществляться:

• по событиям (время, частота, мера, тенденции, причины, последствия);

• по типам социальных групп посетителей парка или населения города (возраст, пол, национальность, семейное положение, вероисповедание);

• по изделиям и материалам (объем, ценность, технические характеристики) или ассортименту древесных и кустарниковых пород;

• по входу-выходу (сбыт продукции, финансы, энергоснабжение, вид деятельности, кадры и т.п.).

Метод анализа проблем используется в случаях, когда причины той или иной проблемы не ясны.

Метод анализа взаимного влияния представляет собой группу различных методов (анализ входа-выхода, анализ баланса, корреляционный и регрессивный анализ и др.), целью которых является выяснение взаимовлияний между изучаемыми факторами и событиями и степенью этого влияния. Например, является ли низкая посещаемость парка следствием его плохого художественного оформления и благоустройства (малые архитектурные формы, освещение, покрытие аллей и др.) или налицо монотонность, неоригинальность подбора древесных и кустарниковых пород?

Метод сравнения; его нельзя применять, используя материалы только по одному парку, одной функциональной зоне парка, а в отдельных случаях – материалы озеленения только одного населенного пункта.

При архитектурных и социально-эстетических исследованиях мы имеем дело со стохастическими величинами. Стохастическая (случайная) величина – это величина, которая может быть, а может и не быть в зависимости от многих факторов. К таким величинам относятся годовое количество осадков, среднегодовые температуры, надои молока, привесы животных, яйценоскость кур, число лиц, заболевших в течение года или сезона гриппом и др.

Всякое научное наблюдение должно сопровождаться четкой хронографией, желательно в специально разработанных бланках и таблицах. Обработка полученных результатов ведется в табличной форме (табл. 9).

 

Таблица 9

Математическая оценка результатов исследований

№№ пп	Значение изучаемого показателя m	Отклонение от среднего значения (m-m0)	Квадратичное отклонение (m-m0)2	Кубическое отклонение (m-m0)3
…
n
	∑m	∑(m-m0)	∑(m-m0)2	∑(m-m0)3

 

Затем вычисляется среднее значение исследуемого параметра:

,

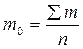где n – генеральная совокупность наблюдений,

m – значение изучаемого параметра.