Основные положения проектирования гибких фундаментов.
До сих пор, при расчете гибких фундаментов совместно с грунтовым основанием применяются эти две теории, которые в соответствии с классификацией Н.А.Цытовича /4/ называются:
теория местных упругих деформаций, основанная на гипотезе Винклера-Циммермана;
теория общих упругих деформаций, основанная на гипотезе упругого полупространства.
Теория местных упругих деформаций основана на гипотезе прямой пропорциональности между давлением и местной осадкой:
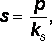 где s – упругая осадка грунта в месте приложения давления интенсивностью p в рассматриваемой точке; ks коэффициент упругости основания (кН/м3), именуемый «коэффициентом постели».
где s – упругая осадка грунта в месте приложения давления интенсивностью p в рассматриваемой точке; ks коэффициент упругости основания (кН/м3), именуемый «коэффициентом постели».
Из приведенного выражения следует, что осадка поверхности основания возникает только в месте приложения давления p и поэтому модель грунта можно представить в виде совокупности отдельно стоящих пружин (рис.1,а).
В действительности на реальном грунтовом основании понижение поверхности наблюдается и за пределами нагруженного участка (рис.1,б), образуя упругую лунку. Кроме того, коэффициент постели не учитывает размеров подошвы фундамента и не является постоянной величиной для данного грунта. Как показали исследования, данная гипотеза дает достаточно достоверные результаты для слабых грунтовых оснований.
Несмотря на отмеченные недостатки метод местных упругих деформаций, на котором базируются расчеты балок и плит на упругом (Винклеровском) основании, позволяя более экономично проектировать гибкие фундаменты с учетом податливости грунтового основания, до сих пор находит довольно широкое применение при расчете ленточных и плитных фундаментов и дает достаточно достоверные результаты, если при выборе величины коэффициенты постели учитывается площадь передачи нагрузки и величина среднего давления га грунт по подошве.
Следует отметить, что широко применяемая на практике программа "Лира/Scad" /5/ для расчета строительных конструкций включает модуль позволяющий рассчитывать гибкие фундаменты, базирующийся в свою очередь на методе местных упругих деформаций.
Теория общих упругих деформаций основана на гипотезе упругого полупространства, согласно которой основание работает как сплошная однородная упругая среда, ограниченная сверху плоскостью и, бесконечно простирающаяся вниз и в стороны. Деформационные свойства упругой среды характеризуются величиной модуля деформации, который не зависит от величины нагрузки под подошвой фундамента, в отличие от коэффициента постели. При нагружении такого упругого основания деформации имеют место не только в месте приложения нагрузки, но и за ее пределами (рис.1,б), что и наблюдается под реальными фундаментами.
Деформация упругого основания по теории общих упругих деформаций определяется с использованием решений теории упругости.
Исходными уравнениями деформаций основания в теории общих упругих деформаций являются:
- для случая плоской деформации – решение Фламана
 - для случая пространственной и осесимметричной деформации – решение Буссинеска
- для случая пространственной и осесимметричной деформации – решение Буссинеска 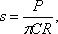 где s осадка упругой полуплоскости или полупространства; Р- сосредоточенная сила для случая пространственной деформации; p погонная полосовая нагрузка для случая плоской деформации:
где s осадка упругой полуплоскости или полупространства; Р- сосредоточенная сила для случая пространственной деформации; p погонная полосовая нагрузка для случая плоской деформации: 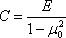 коэффициент деформируемости полупространства; R, x расстояние до рассматриваемой точки ограничивающей плоскости; D постоянная интегрирования.
коэффициент деформируемости полупространства; R, x расстояние до рассматриваемой точки ограничивающей плоскости; D постоянная интегрирования.
Опыт применения данного метода, накопленный при поектировании большого количества ответственных сооружений, показал, что упругое полупространство во многих случаях хорошо моделирует грунтовое основание.
Однако и этот метод имеет определенные недостатки. Основной его характеристикой является модуль деформации. Существующие лабораторные методы не позволяют определять его с достаточной точностью. Испытания грунта в компрессионных приборах дают заниженные значения модуля деформации. Оказалось, кроме того, что модуль деформации имеет различные значения для условий плоской и пространственной деформации.
Кроме того распределение реактивных давлений по теории упругости обладает существенным недостатком: под краями фундамента они становятся бесконечно большими (рис. 2), чего в опытах не наблюдается, поэтому во многих случаях эта модель основания приводит к завышенным внутренним усилиям (моменты и поперечные силы) в конструкции фундаментов.