Примеры решения задач
При решении задач данного раздела, как правило, требуется применять первое начало термодинамики. Для этого следует определить вид процесса, происходящего с газом и применить соответствующие формулы для расчета изменения внутренней энергии и работы газа. В случае произвольного процесса первое начало термодинамики следует записывать в дифференциальной форме, а затем вычислять интегралы, исключая из подынтегральной функции некоторые параметры состояния при помощи уравнения Менделеева – Клапейрона. Аналогично решаются задачи на расчет изменения энтропии системы и определение коэффициента полезного действия. Рассмотрим конкретные примеры.
Задача 1. В двух цилиндрах, имеющих объемы  и
и  находится одинаковый газ при давлениях
находится одинаковый газ при давлениях  и
и  и температурах
и температурах 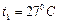 и
и  . Цилиндры соединяют трубкой с краном. Определить, какая температура
. Цилиндры соединяют трубкой с краном. Определить, какая температура  и какое давление
и какое давление  установятся в цилиндрах после того, как кран соединительной трубки будет открыт.
установятся в цилиндрах после того, как кран соединительной трубки будет открыт.
Решение
Внутренние энергии газа в первом цилиндре, газа во втором цилиндре и газа в обоих цилиндрах после смешивания соответственно равны:
 ,
,  ,
,  , (2.3.1)
, (2.3.1)
где  и
и  - количества вещества газов в цилиндрах,
- количества вещества газов в цилиндрах,  - молярная теплоемкость газа при постоянном объеме.
- молярная теплоемкость газа при постоянном объеме.
Согласно закону сохранения энергии
 ,
,
откуда с учетом (2.3.1) следует
 . (2.3.2)
. (2.3.2)
Для определения количества вещества воспользуемся уравнением состояния идеального газа:
 ,
,  . (2.3.3)
. (2.3.3)
Выражая из (2.3.3) количества вещества и подставляя в (2.3.2), получаем
 . (2.3.4)
. (2.3.4)
Подставляя числовые значения, находим
 .
.
Из уравнения состояния для смеси газов
 ,
,
используя (2.3.3) и (2.3.4), находим
 .
.
Задача 2. В длинной гладкой пустой (нет внешнего давления) теплоизолированной трубе находятся два поршня массами  и
и  , между которыми в объеме
, между которыми в объеме  при давлении
при давлении 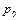 находится двухатомный газ. Поршни отпускают. Определить их максимальные скорости, если масса газа много меньше массы поршней.
находится двухатомный газ. Поршни отпускают. Определить их максимальные скорости, если масса газа много меньше массы поршней.
Решение
Воспользуемся законами сохранения импульса и энергии. Поскольку согласно условию, труба теплоизолирована, газ будет совершать работу над поршнями без теплообмена с окружающей средой за счет внутренней энергии.
Предположим, что расширение газа будет бесконечным, следовательно, его внутренняя энергия будет стремиться к нулю. Тогда по закону сохранения энергии
 , (2.3.5)
, (2.3.5)
где  - начальная внутренняя энергия газа.
- начальная внутренняя энергия газа.
По определению
 , (2.3.6)
, (2.3.6)
где число степеней свободы двухатомной молекулы  . При помощи уравнения состояния идеального газа
. При помощи уравнения состояния идеального газа  можно выразить внутреннюю энергию через объем и давление газа:
можно выразить внутреннюю энергию через объем и давление газа:
 ,
,
следовательно, (2.3.5) преобразуется к виду
 . (2.3.7)
. (2.3.7)
Поскольку по условию масса газа пренебрежимо мала, из закона сохранения импульса следует
 . (2.3.8)
. (2.3.8)
Решая систему уравнений (2.3.7), (2.3.8), находим максимальные скорости поршней
 ,
,  .
.
Задача 3 . Температура некоторой массы 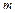 идеального газа молярной массы
идеального газа молярной массы  меняется по закону
меняется по закону  , где
, где  . Найти работу, совершенную газом при увеличении объема от
. Найти работу, совершенную газом при увеличении объема от  до
до  . Поглощается или выделяется энергия в таком процессе?
. Поглощается или выделяется энергия в таком процессе?
Решение
Элементарная работа идеального газа определяется по формуле
 . (2.3.9)
. (2.3.9)
Выразим давление газа при помощи уравнения состояния идеального газа  и уравнения
и уравнения  , заданного по условию. Получаем
, заданного по условию. Получаем
 ,
,
следовательно, (2.3.9) приводится к виду
 . (2.3.10)
. (2.3.10)
Интегрируя (2.3.10) от  до
до  , получаем
, получаем
 .
.
Поскольку, согласно закону расширения газа, с увеличением объема растет температура, совершенная газом работа и изменение его внутренней энергии положительны. Следовательно, по первому началу термодинамики газ должен поглощать тепло.
Задача 4. Азот, находившийся при температуре  , подвергли адиабатному расширению, в результате которого его объем увеличился в
, подвергли адиабатному расширению, в результате которого его объем увеличился в  раз, а внутренняя энергия уменьшилась на 4 кДж. Определить массу азота.
раз, а внутренняя энергия уменьшилась на 4 кДж. Определить массу азота.
Решение
Работа газа при адиабатном расширении определяется по формуле  ,
,
где показатель адиабаты  ,
,  - число степеней свободы двухатомной молекулы.
- число степеней свободы двухатомной молекулы.
Из первого закона термодинамики  следует, что при адиабатном процессе (
следует, что при адиабатном процессе (  )
)
 . (2.3.11)
. (2.3.11)
Учитывая, что по условию  , из (2.3.11) получаем выражение для массы азота
, из (2.3.11) получаем выражение для массы азота
 .
.
Подставляя числовые значения, находим
 .
.
Задача 5. Найти молярную теплоемкость идеального газа, расширяющегося по закону  . При каких значениях
. При каких значениях  теплоемкость будет равна нулю? Бесконечности?
теплоемкость будет равна нулю? Бесконечности?
Решение
Согласно определению молярной теплоемкости
 . (2.3.12)
. (2.3.12)
Воспользуемся первым началом термодинамики
 , (2.3.13)
, (2.3.13)
где внутренняя энергия одноатомного газа
 . (2.3.14)
. (2.3.14)
Для определения элементарной работы газа вычислим дифференциалы от уравнения состояния идеального газа и от заданного по условию закона его расширения:
 (2.3.15)
(2.3.15)
и
 . (2.3.16)
. (2.3.16)
Решая совместно (2.3.15), (2.3.16), получаем
 . (2.3.17)
. (2.3.17)
Тогда из (2.3.12), (2.3.13), (2.3.14), (2.3.17) находим
 .
.
Из условий  и
и  получаем
получаем  и
и  соответственно.
соответственно.
 |
Задача 6. Коэффициент полезного действия цикла 1-2-3-4-1, представленного на рисунке, равен
 . Определить КПД
. Определить КПД  цикла 1-3-4-1.
цикла 1-3-4-1.
Решение
По определению КПД
 . (2.3.18)
. (2.3.18)
Работа, совершенная газом за цикл, равна площади фигуры на диаграмме. Очевидно, что работы газа в циклах 1-2-3-4-1 и 1-3-4-1 связаны друг с другом соотношением  .
.
Участок 1-2 соответствует изохорному нагреванию, а участок 2-3 – изобарному расширению, следовательно, на этих участках газ получает тепло. Участок 3-4 соответствует изохорному охлаждению, а участок 4-1 – изобарному сжатию, следовательно, на этих участках газ отдает тепло. Так как участки 3-4 и 4-1 для обоих циклов одинаковы, количество теплоты  , отдаваемое газом холодильнику в этих циклах одинаково.
, отдаваемое газом холодильнику в этих циклах одинаково.
Поскольку  , из (2.3.18) получаем
, из (2.3.18) получаем
 . (2.3.19)
. (2.3.19)
Подставляя найденное значение в формулу КПД цикла 1-3-4-1, находим
 .
.
 |
Задача 7. С одним молем одноатомного идеального газа совершают циклический процесс 1-2-3-1, изображенный на рисунке. В процессе 2-3 давление газа линейно зависит от объема, причем объем увеличивается вдвое. Состояниям 2 и 3 соответствует одинаковая температура. Найти КПД тепловой машины, работающей по такому циклу.
Решение
Определим при помощи условия соотношения между параметрами газа в состояниях 1, 2 и 3. Согласно уравнению состояния идеального газа для состояний 2 и 3 имеем
 ,
,  . (2.3.20)
. (2.3.20)
Так как  ,
,  , то из (2.3.20) следует
, то из (2.3.20) следует
 ,
,  ,
,  . (2.3.21)
. (2.3.21)
Количество теплоты, полученное газом при изохорном нагревании 1-2 равно
 . (2.3.22)
. (2.3.22)
Определяя параметры линейного уравнения зависимости давления от объема для участка 2-3, получаем
 ,
,
тогда элементарная работа газа на этом участке
 . (2.3.23)
. (2.3.23)
Интегрируя (2.3.23) от  до
до  , получаем
, получаем
 .
.
Так как на участке 2-3 внутренняя энергия газа не меняется, то по первому закону термодинамики
 . (2.3.24)
. (2.3.24)
Следовательно, на этом участке газ также получает тепло. На участке изобарного сжатия газ отдает холодильнику количество теплоты
 . (2.3.25)
. (2.3.25)
Подставляя (2.3.22), (2.3.24), (2.3.25) в определение КПД, находим
 .
.
Задача 8. На сколько возрастет энтропия  воды, находящейся при
воды, находящейся при  , при превращении ее в пар?
, при превращении ее в пар?
Решение
Изменение энтропии системы определяется по формуле
 . (2.3.26)
. (2.3.26)
Количество теплоты, необходимое для нагревания воды, вычисляется по формуле
 , (2.3.27)
, (2.3.27)
где  - удельная теплоемкость воды. Подставляя (2.3.27) в (2.3.26) и интегрируя, находим
- удельная теплоемкость воды. Подставляя (2.3.27) в (2.3.26) и интегрируя, находим
 , (2.3.28)
, (2.3.28)
где 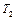 - температура кипения воды.
- температура кипения воды.
Кипение воды происходит при постоянной температуре, поэтому
 , (2.3.29)
, (2.3.29)
где  - удельная теплота парообразования воды.
- удельная теплота парообразования воды.
Из (2.3.26), (2.3.28), (2.3.29), находим изменение энтропии в рассматриваемом процессе
 .
.
Подставим значения:

 .
.