Методика вычисления теоретических частот
1) По выборочным данным строят интервальный ряд распределения.
2) Вычисляют числовые характеристики (параметры) построенного ряда, необходимые для задания конкретного закона распределения. Так, например, для задания нормального закона необходимо найти выборочную среднюю и выборочное среднее квадратическое отклонение, а для задания показательного распределения достаточно найти выборочную среднюю.
3) Вычисляют теоретические вероятности 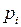 попадания случайной величины X в интервалы (
попадания случайной величины X в интервалы (  ). Так, например, для нормального закона распределения
). Так, например, для нормального закона распределения  ,
,
где Ф(t) – функция Лапласа,  - несмещенная оценка генеральной средней,
- несмещенная оценка генеральной средней,  - несмещенная оценка генерального среднего квадратического отклонения.
- несмещенная оценка генерального среднего квадратического отклонения.
Для показательного распределения теоретические вероятности найдем по формуле
 ,
,
где F(t) – интегральная функция показательного распределения,
 - параметр показательного распределения (
- параметр показательного распределения (  ).
).
Для равномерного распределения теоретические вероятности найдем по формуле  , где l – число частичных интервалов.
, где l – число частичных интервалов.
4) Находят искомые теоретические частоты по формуле  ,
,
где n – объем выборки.