Теоремы двойственности
Двойственность является фундаментальным понятием в теории линейного программирования. Основные результаты теории двойственности заключены в двух теоремах, называемых теоремами двойственности.
Теорема 1 (первая теорема двойственности).
Если одна из пары двойственных задач I и II разрешима, то разрешима и другая, причем значения целевых функций на оптимальных планах совпадают, F(x*) = G(y*), где х*, у* - оптимальные решения задач I и II
Теорема 2 (вторая теорема двойственности).
Планы х* и у* оптимальны в задачах I и II тогда и только тогда, когда при подстановке их в систему ограничений задач I и II соответственно хотя бы одно из любой пары сопряженных неравенств обращается в равенство.
Доказательства теорем опускаем, а на конкретном примере посмотрим связь в паре двойственных задач.
Итак, имеем исходную задачу I, которую мы решили в п. 3.8, и ее оптимальное решение х* = (0, 40, 0, 100) и F(х*) = 700.
Найдем решение двойственной задачи II у* = (у1, у2, у3) из п. 3.9.1, не прибегая к симплекс-методу, а воспользовавшись второй теоремой двойственности и известным оптимальным планом х*.
Рассмотрим выполнение неравенств задачи I при подстановке х* в систему ограничений.
Поскольку 1, 5, 7 неравенства строгие (имеют знак "<" или ">"), то соответствующие им неравенства в задаче II из пары сопряженных обязаны обратиться в равенства. имеем:
или 
т. е. у* = (0, 1, 4) - оптимальное решение.
Заметим, что действительно G(y*) = 400y1 + 300y2 + 100y3 = 400 · 0 + 300 · 1 + 100 · 4 = 700 = F(x*).
Итак, в силу второй теоремы двойственности мы очень быстро нашли оптимальное решение задачи II, пользуясь условием обращения в равенство хотя бы одного из пары сопряженных неравенств в системах ограничений двойственных задач.
Между переменными исходной задачи и переменными двойственной существует глубокая связь. А именно: после приведения обеих задач I и II к каноническому виду основные и дополнительные переменные задач соответствуют друг другу следующим образом:
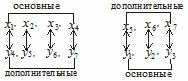
Установив такую связь, внимательный читатель заметит, что, решив задачу I симплекс-методом и получив последнюю симплекс-таблицу (табл. 3.15), мы фактически решим и задачу II.
Запишем таблицу 3.15, учитывая соответствие между переменными хi и yj (табл. 3.16).
Таблица 3.16
| у4 | у2 | у6 | у3 | |||
| базисные | -х1 | -х6 | -х3 | -х7 | свободные | |
| у1 | х5 | |||||
| у5 | х2 | |||||
| у7 | х4 | |||||
| -F |
В силу соответствия и II теоремы двойственности переменные у1, у5, у7 обязаны равняться 0, т. к. х5, х2, х4>0 строго. А переменные у4, у2, у6, у3 принимают значения из индексной строки 1, 1, 1, 4 соответственно, т. к. им соответствующие переменные х1, х6, х3, х7 = 0, как свободные. Итак, из последней таблицы задачи II, не проводя даже никаких вычислений и пользуясь лишь соответствием переменных:
у* = (у1*, у2*, у3*, у4*, у5*, у6*, у7*) = (0, 1, 4, 1, 0, 1, 0).
Мы научились по решению исходной задачи находить решение двойственной. Это оказалось возможно благодаря глубокой связи между переменными хi и yj. Осталось разобраться, каково экономическое содержание этих взаимосвязей.
49 Предприятие выпускает n видов продукции (P 1,P2, …,Pn) используя для производства mвидов ресурсов (S 1,S2, …,Sm). Известны данные о нормах расхода ресурсов на единицу продукции каждого вида и их запасах на предприятии, т.е.
: 
– норма расхода ресурса Si для производства единицы продукции Pj; 
– запас ресурса Si на предприятии.
Цена единицы продукции Pj составляет 
.
Необходимо составить такой план производства продукции, при котором выручка от ее реализации была бы максимальной.
Обозначим через 
– объем продукции Pj, запланированный к производству – искомые величины. Тогда математическая модель данной задачи будет иметь следующий вид:
(8.1)
(8.2)
(8.3)
Полученная задача, является задачей линейного программирования, записанной в стандартной форме. Для удобства задачу (8.1)–(8.3) можно представить в компактной форме:
(8.4)
(8.5)
(8.6)
В итоге математическая модель задачи планирования производства может быть сформулирована следующим образом: составить такой план производства продукции X=(x1,x2, …,xn), удовлетворяющий системе ограничений (8.4), условию (8.5), при котором целевая функция (8.6) принимает наибольшее значение.
Предположим, что некоторая организация решила закупить у предприятия ресурсы S1,S2, …,Sm и ей необходимо определить оптимальные цены на эти ресурсы y1,y2, …,ym, исходя из следующих условий:
1) общая стоимость ресурсов для закупающей организации должна быть минимальной;
2) за каждый вид ресурса предприятию надо уплатить не менее той суммы, которую оно может получать при переработке данного вида ресурса в готовую продукцию.
Исходя из условия 1 покупающая организация заинтересована в том, чтобы затраты на все ресурсы Z в количествах b 1,b2, …,bm по ценам соответственно y1,y 2, …,ym были минимальными, т.е.
. (8.7)
Исходя из условия 2 для удовлетворения требований продавца стоимость ресурсов, потребляемых при изготовлении единицы продукции каждого вида, должна быть не меньше ее цены, т.е.
(8.8)
По свой сущности переменные yi не отрицательные, т.е.
. (8.9)
Таким образом, математическая модель для закупающей организации будет иметь следующий вид:
(8.10)
, (8.11)
(8.12)
Сравним математические модели (8.1) – (8.3) и (8.7) – (8.9):
1) число неизвестных одной задачи равно числу ограничений другой;
2) матрица коэффициентов системы ограничений одной задачи получается путем транспонирования матрицы коэффициентов системы ограничений другой задачи;
3) неравенства в системах ограничений имеют противоположный смысл;
4) свободные числа системы ограничений одной из задач являются коэффициентами при неизвестных в целевой функции другой задачи и наоборот;
5) целевые функции в задачах имеют противоположный смысл.
Задачи линейного программирования, обладающие пятью вышеуказанными формальными признаками, называют симметричнойдвойственной парой, причем одну из них (исходную) принимают в качестве основной, а другую – двойственной.
В теории линейного программирования выделяют также и несимметричныедвойственныепары, к примеру, если системы ограничений задач содержат ограничения-равенства и/или отсутствуют условия неотрицательности переменных.
Правила построения двойственной пары:
1) Знаки неравенств в системе ограничений исходной задачи приводятся в соответствие с ее целевой функцией, т.е. если она минимизируется, то неравенства должны иметь вид «≥», а если максимизируется, то «≤». Данный принцип распространяется и на двойственную задачу.
2) Определяется число неизвестных параметров двойственной задачи, равное числу ограничений исходной задачи.
3) Определяется область допустимых значений каждой из переменных двойственной задачи исходя из следующего правила:
каждому i-му ограничению-неравенству исходной задачи соответствует i-ая переменная двойственной задачи, удовлетворяющая условию неотрицательности; а каждому i-му ограничению-равенству исходной задачи соответствует i-ая переменная двойственной задачи, неограниченная по знаку.
4) Определяется матрица коэффициентов системы ограничений двойственной задачи путем транспонирования матрицы коэффициентов системы ограничений исходной задачи.
5) Определяются свободные числа системы ограничений двойственной задачи, равные коэффициентам при неизвестных в целевой функции исходной задачи.
6) Записывается система ограничений двойственной задачи, причем вид каждого ограничения определяется исходя из следующего правила:
каждой j-ой переменной исходной задачи, удовлетворяющей условию неотрицательности, соответствует j-ое ограничение- неравенство двойственной задачи (вид неравенства устанавливается в соответствие с принципом сформулированном в правиле 1 и исходя из того, что целевая функция двойственной задачи имеет противоположный целевой функции исходной задачи смысл (правило 7)); а каждой j-ой переменной исходной задачи, неограниченной по знаку, соответствует j-ое ограничение-равенство двойственной задачи.
7) Определяются коэффициенты при неизвестных целевой функции двойственной задачи, равные соответствующим свободным числам системы ограничений исходной задачи. Затем записывается целевая функция двойственной задачи, причем она будет иметь противоположный целевой функции исходной задачи смысл, т.е. минимизироваться, если целевая функция исходной задачи максимизируется и, наоборот.