Решение

Напомним (С 2.3), что треугольная нагрузка имеет равнодействующую равную , которая приложена на одной трети длины участка от основания треугольника.

Определяем реакции ( С 2.4, С 2.5, К 2.2, К 2.10).

; ;

;

; ;

;

Аналитические выражения для Q_y и М_х легче записывать, если рассекая треугольную нагрузку произвольным сечением, отбрасывать часть балки с трапецеидальной частью нагрузки. Поэтому на 1-м участке будем рассматривать левую часть балки, на 2-м и 3-м участках – правую часть балки.

 

1-й участок 0 ≤ 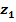≤ 3 м

Сечением, расположенным на расстоянии 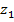от края балки отсекается нагрузка в виде треугольника с основанием 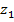и высотой , причем высота зависит от расположения сечения, то есть а равнодействующая нагрузки действует на расстоянии от сечения.

 

Для начала определим как зависит от 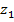. Для этого приравняем отношение катетов двух подобных треугольников:

Откуда .

Запишем выражения для Q_y и М_х .

(квадратная парабола).

Квадратную параболу следует строить по трем точкам ( К 2.35).

;

;

(кубическая парабола).

 

Точно построить кубическую параболу можно лишь по четырем точка.

, ;

, ;

 

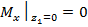В любом случае следует помнить, что касательная к графику функции горизонтальна в том сечении, где на предыдущей эпюре значение равно нулю. Используя это правило, можно в ряде случаев пропускать подсчет значений усилий в промежуточных сечениях участка.

 

2-й участок 1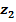м ≤ ≤ 4 м

Ищем закон изменения из подобия треугольников:

, откуда

;

Тогда

;

;

Строим график – квадратную параболу.

, ;

Касательная горизонтальна на правой границе участка при где при .

 

Ищем точку пересечения с осью из условия

;

;

Откуда

;

Отбрасывая отрицательный корень ,

получаем

Строим график – кубическую параболу, выпуклостью которой обращена вверх (К 2.28).

;