Ленгмюра

Количественной характеристикой процесса адсорбции является степень заполнения адсорбционных центров θ(t)=N_a(t)/N_ц, где N_а и N_ц(t) – концентрация адсорбционных центров и адсорбированных молекул в момент времени t.

Рассмотрим кинетику монослойной адсорбции, при которой N_a < N_ц так что θ ≤ 1. Скорость изменения концентрации адсорбированных молекул равняется разности между плотностями потока адсорбируемых частиц и потока десорбируемых частиц

Как известно из молекулярно-кинетической теории газов, при температуре Т из парогазовой фазы, имеющей для рассматриваемого компонента парциальное давление р, на любую поверхность падает поток молекул с массой m, имеющий плотность

Часть этих молекул отражается от поверхности, а другая часть адсорбируется ею, что феноменологически учитывается коэффициентом конденсации α, характеризующим вероятность закрепления падающей молекулы на поверхности. Естественно предположить, что зависимость коэффициента конденсации от степени заполнения адсорбционных центров описывается функцией α(θ) = α_о(1-θ), такой, что α = α_о<1 для свободной поверхности (при θ = 0) и α = 0 для полностью заполненного монослоя (при θ = 1). Тогда плотность потока адсорбируемых молекул равняется

Число молекул, десорбируемых с единицы площади в единицу времени (т. е. плотность потока ), прямо пропорционально концентрации молекул N_a = N_цθ, адсорбированных в данный момент на поверхности, и обратно пропорционально среднему времени τ_а их жизни вадсорбированном состоянии:

Подстановка (2) и (3) в равенство (1) дает уравнение для θ(t):

Использовав выражения для ν приведем уравнение к окончательной форме:

которая имеет вид уравнения релаксации, описывающего кинетику процесса физической адсорбции. Уравнение (4) содержит две постоянные времени:

а) постоянную , зависящую от давления р в форме:

где с учетом того, что

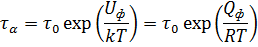
введена температурно-зависимая константа

б) эффективное время релаксации процесса адсорбции

Из приведенных формул видно, что с увеличением давления р обе постоянные уменьшаются. Влияние температуры проявляется более сложным образом, так как нормировочная величина 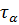сама зависит от Т.

Решение уравнения (4) при начальном условии θ(0) = 0 имеет вид

где стационарная степень заполнения , достигаемая при t→∞, дается выражением

Рис. 6. Временная зависимость нестационарной степени заполнения адсорбционных центров θ0 при разных значениях параметра bр - 0,5 (кривая 1), 1 (кривая 2), 2 (кривая 3), 3 (кривая 4), 5 (кривая 5), 10 (кривая 6).

которое является функцией температуры Т и давления р. Соотношение (6) принято называть уравнением Ленгмюра.

Зависимость от параметра bр, рассчитанная по формуле (6), приведена на рис.6. Таким образом, с ростом давления в газовой фазе стационарная степень заполнения возрастает, стремясь к единице, в то время как эффективное время релаксации уменьшается от значения 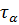, приближаясь к нулю. Следовательно, при более высоких давлениях адсорбционные центры заполняются до больших значений за более короткое время.