VI.3. Поля, создаваемые ограниченными колеблющимися источниками

Итак, как было показано в предыдущем параграфе, излучение электромагнитных волн описывается решениями в виде запаздывающих потенциалов. В результате, имеем следующие выражения для векторного и скалярного потенциалов (6.3), (6.4):

, . (6.31)

Систему зарядов и токов, изменяющихся во времени, всегда можно разложить на гармоники с помощью рядов или интегралов Фурье (П6.1) и рассматривать в отдельности каждую гармонику. Поэтому без ущерба для общности мы может рассматривать потенциалы, поля и излучение ограниченной системы зарядов и токов, изменяющихся по времени по гармоническому закону:

, . (6.32)

Для нахождения истинных физических величин следует брать действительную часть этих выражений. Предполагается, что электромагнитные потенциалы и поля имеют такую же временную зависимость. При гармонической временной зависимости (6.32) решения (6.31) принимают вид

, , (6.33)

где , - длина волны гармонического колебания с циклической частотой , распространяющегося со скоростью c (для определённости мы будем иметь в виду случай вакуума).

Магнитное поле определяется соотношением

, (6.34)

а электрическое поле вне источников равно . (6.35)

При заданном распределении токов поля могут быть найдены, если вычислен интеграл (6.33). Будем в дальнейшем предполагать, что источники сосредоточены в очень малой по сравнению с длиной волны области. Если размеры источника имеют величину порядка d, а длина волны и , то представляют интерес три области

ближняя (статическая) зона: ,

промежуточная (индукционная) зона: ,

дальняя (волновая) зона: .

Если мы рассмотрим поля вдали от источника , не делая никаких предположений об отношении r к , то в интеграле (6.33) можно положить

, (6.36)

где - единичный вектор в направлении . При этом векторный потенциал принимает вид

. (6.37)

Предполагая, что и , можно разложить экспоненту и знаменатель в ряд по :

. (6.38)

Подставив это разложение в (6.21), получим m-й член ряда для :

, (6.39)

где коэффициенты полинома - некоторые целые числа. Это выражение позволяет определить радиальную зависимость поля в общем случае. В ближней зоне, где , преобладающим является последний член полинома, так что векторный потенциал стремится к пределу

,

не зависящему от волнового числа k. Таким образом, поля в ближней зоне являются квазистатическими: они гармонически изменяются по времени как , но во всех других отношениях имеют статический характер.

В дальней зоне, где , доминирующим членом полинома в (6.39) будет первый член, и для векторного потенциала получаем

. (6.40)

В этом приближении векторный потенциал дает расходящуюся сферическую волну. Легко показать, что в дальней зоне поля (6.34) и (6.35) перпендикулярны радиус-вектору и спадают как 1/r. Таким образом, они представляют собой поля излучения. Амплитуда m-го члена разложения в волновой зоне равна

.

Так как 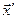имеет величину порядка d, а произведение kd, по предположению, мало по сравнению с единицей, то очевидно, что последовательные члены в разложении быстро уменьшаются с номером m. Следовательно, излучение источника определяется в основном первым неисчезающим членом разложения (6.38). Перейдем теперь к более детальному анализу полей, соответствующим последовательным членам разложения.