VI.2. Собственные функции скалярного волнового уравнения
Волновые уравнения (6.3), (6.4), (6.7) имеют одинаковую структуру
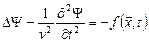 , (6.20)
, (6.20)
где  дает распределение источников, а v представляет собой скорость распространения волн в среде.
дает распределение источников, а v представляет собой скорость распространения волн в среде.
Для решения уравнения (6.20) полезно найти сначала функцию Грина, удовлетворяющую уравнению
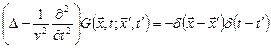 , (6.21)
, (6.21)
Решение уравнения (6.20) в неограниченном пространстве без граничных поверхностей выражается через G интегралом
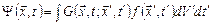 . (6.22)
. (6.22)
Нужно также потребовать, чтобы функция Грина удовлетворяла определенным граничным условиям, которые задаются физическими требованиями.
Функция Грина, удовлетворяющая уравнению (6.21), зависит только от разностей координат 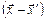 и времен
и времен 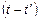 . Для нахождения G представим обе части уравнения (6.21) в виде интегралов Фурье (П6.1). Дельта-функцию в правой части можно представить следующим образом (П6.2):
. Для нахождения G представим обе части уравнения (6.21) в виде интегралов Фурье (П6.1). Дельта-функцию в правой части можно представить следующим образом (П6.2):
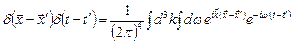 . (6.23)
. (6.23)
Соответственно запишем функцию Грина в виде
 . (6.24)
. (6.24)
Функцию 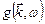 легко определить, подставив (6.23) и (6.24) в уравнение (6.21). При этом получаем
легко определить, подставив (6.23) и (6.24) в уравнение (6.21). При этом получаем
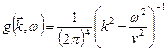 . (6.25)
. (6.25)
При подстановке 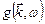 в (6.24) и последующим интегрированием по
в (6.24) и последующим интегрированием по 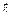 и
и  мы сталкиваемся с особенностью подынтегрального выражения при
мы сталкиваемся с особенностью подынтегрального выражения при 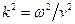 . Решение (6.25) имеет смысл только в том случае, если мы знаем правила обращения с этой особенностью, которые можно получить только из физических соображений.
. Решение (6.25) имеет смысл только в том случае, если мы знаем правила обращения с этой особенностью, которые можно получить только из физических соображений.
Функция Грина, удовлетворяющая волновому уравнению (6.21), представляет собой волновое возмущение, вызванное точечным источником, находящимся в точке 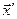 и излучающим только в течение бесконечно малого интервала времени при
и излучающим только в течение бесконечно малого интервала времени при 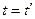 . Мы знаем, что такое возмущение распространяется со скоростью v в виде расходящейся сферической волны. Следовательно, необходимо потребовать, чтобы наше решение для G обладало следующими свойствами:
. Мы знаем, что такое возмущение распространяется со скоростью v в виде расходящейся сферической волны. Следовательно, необходимо потребовать, чтобы наше решение для G обладало следующими свойствами:
а)  всюду при
всюду при  (условие причинности),
(условие причинности),
б) G представляет собой расходящуюся волну при 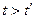 .
.
Интеграл по переменной  в формуле (6.8) имеет вид:
в формуле (6.8) имеет вид:
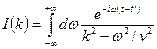 . (6.26)
. (6.26)
Вычисление этого интеграла может быть произведено с помощью теории вычетов. Подынтегральное выражение в (6.26) регулярно при любых комплексных значениях  , за исключением двух полюсов при
, за исключением двух полюсов при 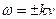 . Если
. Если 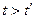 и
и 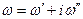 , где
, где  вещественны, то
вещественны, то 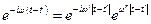 , причем
, причем  в нижней полуплоскости комплексного переменного
в нижней полуплоскости комплексного переменного  (т.е. при
(т.е. при 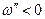 ). Поэтому, если выбрать контур интегрирования в виде отрезка вещественной оси, замыкающего полуокружностью в нижней полуплоскости, то интеграл по этой окружности будет содержать экспоненциально убывающий при
). Поэтому, если выбрать контур интегрирования в виде отрезка вещественной оси, замыкающего полуокружностью в нижней полуплоскости, то интеграл по этой окружности будет содержать экспоненциально убывающий при 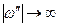 множитель и, значит, в пределе обратится в нуль. Аналогичное условие будет выполняться при
множитель и, значит, в пределе обратится в нуль. Аналогичное условие будет выполняться при  для контура с замыкающей полуокружностью, проведенной в верхней полуплоскости. Для того, чтобы G удовлетворяло условию причинности а), нужно, чтобы внутри такого верхнего контура особенностей подынтегральной функции не было. Поэтому упомянутые выше полюсы следует сместить на бесконечно малое расстояние вниз от вещественной оси, полагая
для контура с замыкающей полуокружностью, проведенной в верхней полуплоскости. Для того, чтобы G удовлетворяло условию причинности а), нужно, чтобы внутри такого верхнего контура особенностей подынтегральной функции не было. Поэтому упомянутые выше полюсы следует сместить на бесконечно малое расстояние вниз от вещественной оси, полагая  . Вычисляя интеграл по теореме Коши при
. Вычисляя интеграл по теореме Коши при 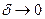 , получаем следующий результат:
, получаем следующий результат:
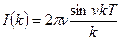 , (6.27)
, (6.27)
где  . С помощью (6.24), (6.25) и (6.27), производя интегрирование по углам, получим
. С помощью (6.24), (6.25) и (6.27), производя интегрирование по углам, получим
 . (6.28)
. (6.28)
Здесь  . Теперь используем четность подынтегральной функции по аргументу k и будем интегрировать от
. Теперь используем четность подынтегральной функции по аргументу k и будем интегрировать от  до
до  . Заменяя переменную k на
. Заменяя переменную k на  , мы может представить (6.28) в виде:
, мы может представить (6.28) в виде:
 (6.29)
(6.29)
Здесь использована формула (П6.2) и то обстоятельство, что  (
(  ). Эта функция Грина называется запаздывающей функцией Грина, что отражает естественную причинную последовательность при распространении волнового возмущения: Эффект, наблюдаемый в точке
). Эта функция Грина называется запаздывающей функцией Грина, что отражает естественную причинную последовательность при распространении волнового возмущения: Эффект, наблюдаемый в точке  в момент времени
в момент времени  , вызывается возмущением, которое произошло в точке
, вызывается возмущением, которое произошло в точке 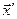 в более раннее (так называемое запаздывающее) время
в более раннее (так называемое запаздывающее) время  .
.
Решение волнового уравнения (6.20) в отсутствии границ имеет вид:
 .
.
Производя интегрирование по  , мы получаем так называемое запаздывающее решение
, мы получаем так называемое запаздывающее решение
 . (6.30)
. (6.30)