АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Рассматриваемые вопросы:
1. Образование аксонометрических осей.
2. Виды аксонометрических проекций.
3. Теорема Польке. Основная теорема аксонометрии.
4. Построение многогранников в аксонометрии.
5. Построение окружности в аксонометрии.
6. Выбор аксонометрических проекций.
Рассмотренные в предыдущих главах ортогональные проекции находят широкое распространение в технике при составлении чертежей. Такие чертежи выполняются достаточно просто, сохраняя метрические характеристики оригинала. Мы можем получить полное представление о внешней и внутренней форме изображаемого предмета, если дополним их вспомогательными видами, разрезами сечениями. Наряду с перечисленными достоинствами ортогонального проецирования этот метод имеет существенный недостаток. Чтобы получить пространственный образ изображаемого предмета в ортогональных проекциях, приходится одновременно рассматривать две, три, а иногда и больше проекций, что замедляет и затрудняет мысленное воспроизведение образа геометрической фигуры.
Чтобы получить обратимый чертеж (чертеж, обеспечивающий взаимную однозначность между точками, принадлежащими проецируемой фигуре и ее проекции), необходимо дополнить его проекцией декартовой системы координат, к которой предварительно была отнесена проецируемая фигура, и указать проекцию не только точки А, но и одной из ее ортогональных проекций.
Такой способ получения чертежа называют аксонометрическим, а полученное с его помощью однопроекционное обратимое отображение геометрической фигуры аксонометрической проекцией, или аксонометрией.
Проекция фигуры на одну плоскость представлена на рис. 68.
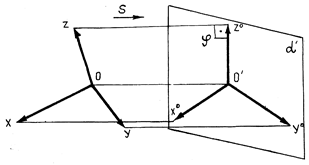
Рис. 68. Образование
координатных осей
На плоскость a спроецирована ортогональная система координат 0xyz. Координатные оси х, у, z спроецируются на плоскость a' в прямые х°, у°, z°, которые называют аксонометрическими осями. В общем случае длина отрезков осей координат в пространстве не равна длине их проекций. Искажение отрезков осей координат при их проецировании на плоскость a характеризуется так называемыми коэффициентами искажения.
Коэффициентом искажения называется отношение длины проекции отрезка оси на плоскости a к его истинной длине. Так, искажения по оси х u = 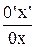 , по оси y v =
, по оси y v = 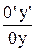 и по оси z' w =
и по оси z' w = 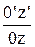 (рис. 69).
(рис. 69).
В зависимости от соотношения коэффициентов искажения аксонометрических проекций могут быть:
1) изометрическими, если коэффициенты искажения по всем трем осям равны между собой; u = v = w.
2) диметрическими, если коэффициенты искажения по двум любым осям равны между собой, а по третьей – отличаются от первых двух. Например, u = w ¹ v.
3) триметрическими, если все три коэффициента искажения по осям различны, т.е. u ¹ v ¹ w, u ¹ w.
Аксонометрические проекции различаются также и по углу j, который образуется проецирующим лучом с плоскостью проекций a'. Если
j ¹ 90°, то аксонометрическая проекция называется косоугольной, а если
j = 90°, – прямоугольной. Естественно, что эти проекции могут быть как прямоугольными, так и косоугольными (рис. 69).