Взаимное пересечение поверхностей

 

Пересечение соосных поверхностей вращения – поверхностей, имеющих общую ось вращения.

Соосные поверхности пересекаются по окружностям. Плоскости этих окружностей всегда ^ к оси вращения. Доказательство см. на рис. 60.

 

 

 

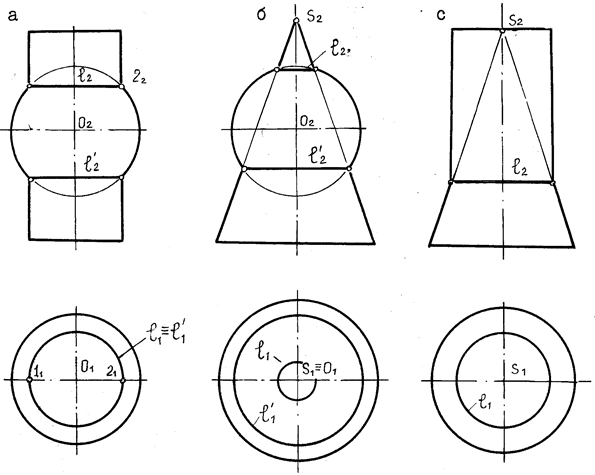
Рис. 60. Пересечение соосных поверхностей

 

 

Доказательство: (.)1 и (.)2 – пересечение образующих поверхностей принадлежит одновременно двум поверхностям. При их образовании поверхности описывают окружности. Причем окружностей столько, сколько точек пересечения образующих. Окружность принадлежит одновременно двум поверхностям, следовательно, это и есть линия их пересечения
(рис. 60).

Теорема 1: Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекаются и еще по одной плоской кривой.

 

		Вывод: Проекции пространственной линии всегда находятся в пределах площади наложения одноименных проекций пересекающихся поверхностей

 

Рис. 61. Алгоритм решения задач на пересечение поверхностей

 

 

Рис. 62. Построение линии пересечения с помощью посредников:

а – секущих плоскостей; б – общий способ решения;

в – эксцентрические сферы; г – концентрические сферы