Закон Максвелла о распределении молекул идеального газа по скоростям
В газе, находящемся в состоянии равновесия, установится некоторое стационарное (не меняющееся со временем) распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Такой закон был теоретически выведен Максвеллом в 1859 г. и был опубликован в 1860 г.
При выводе этого закона Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что внешние поля на газ не действуют.
Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Различают три формы записи распределения Максвелла. Мы изучим одну из них.
1.6.1. Распределение Максвелла по модулю скорости молекул
Обозначим через dNv число молекул, скорости которых лежат в интервале от v до v+dv, тогда dNv/N – характеризует относительное число этих молекул. Принято вводить функцию распределения молекул по скоростям
 . (24)
. (24)
Максвелл показал, что эта функция имеет вид
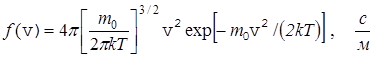 . (25)
. (25)
Функция  характеризует плотность вероятности того, что скорость молекулы равна v, и поэтому эта функция удовлетворяет условию нормировки
характеризует плотность вероятности того, что скорость молекулы равна v, и поэтому эта функция удовлетворяет условию нормировки
 (26)
(26)
|
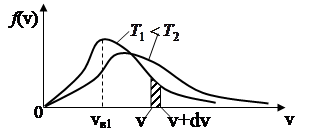 Используя функцию распределения, можно найти относительное число молекул DN/N, скорости которых лежат в интервале от v1 до v2
Используя функцию распределения, можно найти относительное число молекул DN/N, скорости которых лежат в интервале от v1 до v2
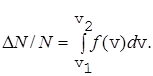 (27)
(27)
Анализ (24) показывает, что вид функции зависит от массы молекулы m0 и от температуры Т.
На рис.4 представлен вид функции f(v) для двух температур. Характерно, что f(v), начинаясь от нуля, достигает максимума при vВ и затем асимптотически стремится к нулю.
Относительное число молекул dNV/ N , скорости которых лежат в интервале от v до v+dv находится как площадь dS заштрихованной полоски на рис. 4. Площади, ограниченные кривыми, согласно (26), одинаковы и равны единице.
Скорость, при которой функция распределения молекул по скоростям максимальна, называется наиболее вероятной скоростью vB. Исследование (24) на максимум позволило найти наиболее вероятную скорость молекул
vB=  . (28)
. (28)
Из формулы (28) следует, что при повышении температуры максимум f(v) сместится вправо, в сторону больших скоростей.
Кроме наиболее вероятной и средней квадратичной скорости молекул газа, которые определяются по формулам (28) и (18), используется также средняя скорость молекул <v> или средняя арифметическая скорость. Она определяется по формуле
<v>=  (29)
(29)
Подставляя f(v) [cм.(24)] и интегрируя , получим
<v>=  . (30)
. (30)
Итак существуют три формулы для определения скорости молекул газа: (18), (28), (30). Согласно этим формулам
vB::<v> :<vKB>=  :
: 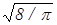 :
:  =1: 1,13 : 1,22. (31)
=1: 1,13 : 1,22. (31)
Таким образом, средняя и средняя квадратичная скорости превышают наиболее вероятную скорость на 13 и 22 % соответственно, т.е. отличие не очень большое.
Исходя из распределения молекул по скоростям (24), можно найти распределение молекул газа по кинетическим энергиям поступательного движения молекул Wк=m0v2/2. Это распределение характеризуется функцией f(Wк), которая вводится аналогично f(v)
 , 1/Дж (32)
, 1/Дж (32)