Опытная проверка законов Малюса и Брюстера
Цель работы: изучить явление поляризации света; опытным путем проверить законы Малюса и Брюстера.
3.1 Краткие теоретические сведения
В волновом процессе, то есть в процессе распространения колебаний, есть два характерных направления: направление колебаний и направление их распространения. Если эти направления совпадают, то волны называют продольными, а если они являются взаимно перпендикулярными, то волны - поперечные. Поскольку в поперечных волнах есть выделенные направление колебаний и плоскость колебаний (плоскость, проведенная через направление колебаний и направление распространения), их можно поляризовать. Поляризацией называется явление организации колебаний в волновом процессе. В реальной поперечной волне колебания могут происходить в разнообразных направлениях (перпендикулярных направлений к направлению распространения есть множество) и явление поляризации заключается в превращении такого неорганизованного волнового процесса в волну с одним направлением колебаний. Волна, поляризуемая таким образом, называется линейно-, или плоско-поляризованной, а устройство, которое выполняет такое превращение, называется поляризатором.
Если налагаются два волновых плоско-поляризованных когерентных процесса, колебания в которых является взаимно перпендикулярными, то результатом сложения таких колебаний, как известно (лаб. раб. 55), есть эллипс, который в волновом процессе смещается со скоростью волны – возникнет эллиптически-поляризованная волна. Такая волна может быть изображена в виде эллиптической спирали. Конечно, основным типом поляризации волн является линейная поляризация.
Волновая оптика рассматривает свет как электромагнитные поперечные волны, частотного диапазона от 0,4 до 0,76×1015 Гц. Известно, что магнитное поле электромагнитной волны не взаимодействует с прозрачными средами, где распространяется свет. По этой причине рассматривается только электрическое поле электромагнитной волны, а напряженность электрического поля электромагнитной волны называют световым вектором. Соответственно свет в волновой оптике представляется как процесс распространения колебаний светового вектора. Световой вектор перпендикулярен волновому вектору, то есть направлению распространения света, поэтому свет должен поляризоваться, что и подтверждает опыт. Поляризацией света называется явление организации колебаний его светового вектора. Исходя из того, что свет, который посылается Солнцем, накаленными телами и другими источниками являются результатом несогласованного излучения множества атомов, то направления колебаний светового вектора в нем с ровной вероятностью представлены во всех направлениях. Такой свет называется естественным. В линейно поляризованном свете представлены колебания только одного направления. Графическое изображение естественного и линейно-поляризованного света приведено на рис 3.1. Здесь изображен естественный
 |
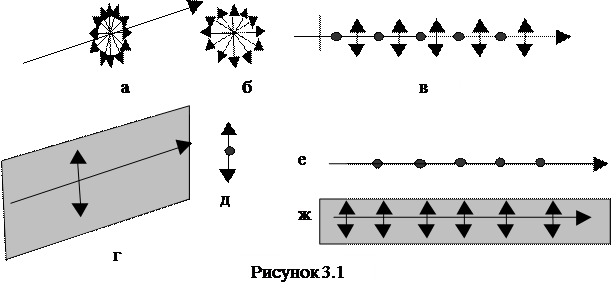неполяризованный свет рис. 3.1 а, б, в и поляризованный рис. 3.1 г, д, е, ж. В свете с поляризацией, изображенном на рис. 3.1 е световой вектор имеет колющую, а на рис. 3.1 ж гладящую компоненты светового вектора.
Как известно, поляризация, в том числе и поляризация света, происходит с помощью поляризаторов. Поляризатор пропускает свет с одним направлением колебаний и полностью задерживает колебание в перпендикулярном направлении. Если колебания происходят в направлении, составляющем угол j с направлением пропускания (рис. 3.2), то их можно разложить на параллельную АII = А cosj и перпендикулярную А^ = А sinj составляющие.
Первые колебания проходит через поляризатор, а вторые полностью задерживаются им. Интенсивность света пропорциональна квадрату амплитуды, поэтому интенсивность поляризованного света, прошедшего через поляризатор, который называется в данном случае анализатором,
Iа ~ (АII)2 = А2 cos2j ~ Ip cos2j.
Соотношение
(3.1)
называется законом Малюса: интенсивность света, прошедшего через анализатор, равняется произведению интенсивности падающего поляризованного света на квадрат косинуса угла между направлением колебаний светового вектора падающего света и направлением пропускания анализатора.
Если на поляризатор падает естественный свет, то в нем представлены колебания произвольных направлений и 0 £ j £ 2p, поэтому интенсивность света после поляризатора Ір = І0 <cos2j> = 0,5І0,, где <cos2j>=0,5 среднее значение квадрата косинусов углов, а І0 – интенсивность естественного света до поляризатора. Если естественный свет проходит через систему “поляризатор – анализатор” (рис. 3.3), то имеет место соотношение:
 |
(3.2)
|
Явление поляризации света наблюдается при отражении от прозрачных диэлектриков и при прохождении его через прозрачные анизотропные кристаллы, то есть через кристаллы, оптические свойства которых зависят от направления, в том числе и направления колебаний светового вектора.
Наблюдая прохождение света через границу раздела прозрачных диэлектриков (вода, стекло, лак и прочее), Брюстер заметил, что отраженный и преломленный свет частично поляризованы. Частично поляризованным называется свет, в котором представлены колебания разных направлений, но их интенсивность зависит от направления. Если пропустить такой свет через анализатор, то при повороте анализатора вокруг направления распространения интенсивность света будет изменяться от Іmах до Іmin. Физическая величина 
определяет степень поляризации. Брюстер показал, что степень поляризации зависит от угла падения света и, если угол между отраженным и преломленным лучом составляет 90°, отраженный свет полностью, а преломленный максимально поляризованы (рис. 3.4). Колебания светового вектора в отраженном свете происходят в направлении, перпендикулярном к плоскости падения света, а преломленный свет при этом максимально поляризован с преимуществом колебаний в плоскости падения (см. рис. 3.4). При таком угле падения, который называется углом Брюстера, g = 90°- b = 90°- a, имеем утверждение, которое носит н
азвание закона Брюстера:
(3.3)
где n1 и n2 – абсолютные показатели преломления света первой и второй по ходу луча сред.
Прохождение света через оптически анизотропные среды сопровождается явлением двойного лучепреломления. Оптическую анизотропию имеют все прозрачные кристаллы, кроме кристаллов кубической симметрии типа кристаллов NaCl. Световой поток, падающий на такой кристалл, разделяется в нем на два потока. Один из них подчиняется законам геометрической оптики и называется обыкновенным, другой не подчиняется этим законам и называется необыкновенным. Необыкновенные лучи не принадлежат плоскости падения, их показатель преломления зависит от направления колебаний и изменяется при повороте кристалла вокруг направления падения света. В кристалле существует один, или два направления, в которых двойное преломление отсутствует. Эти направления определяют главные оптические оси кристаллов. Соответственно кристаллы могут быть одноосные, или двухосные. В двухосном кристалле оба световых потока необыкновенные. Плоскость, которую определяет падающий луч и направление главной оптической оси, поставленное в точку падения луча, называют главной оптической плоскостью кристалла.
Оба световых потока полностью линейно-поляризованные во взаимно-перпендикулярных направлениях: необыкновенный световой поток имеет колебание светового вектора в главной оптической плоскости, а обыкновенный – в направлении, перпендикулярном к ней. Эти потоки могут идти различными путями с разными скоростями. Если один из этих потоков отделить, то можно получить линейно поляризованный свет.
Существуют кристаллы, в которых обыкновенный световой поток поглощается значительно интенсивнее, чем необыкновенный - явление дихроизма. Кристалл, толщина которого составляет доли миллиметра, полностью поглощает обыкновенный поток, а на выходе получается свет полностью линейно поляризованный, то есть выделение необыкновеннного потока происходит естественно. Вышедший поляризованный свет имеет окраску, характерную для данного кристалла,. Явление дихроизма характерно для кристаллов турмалина (свет выходит зеленоватого оттенка), йодистого хинина (коричневого), герапатита (черный оттенок) и других. Мелкие кристаллики таких веществ напыляются с определенной ориентацией оптических осей на полимерные пленки, которые используются как поляризаторы и называются поляроидами (поляроидные пленки).
Обыкновенный и необыкновенный световые потоки некогерентные, поэтому при выходе из кристалла потоки, которые накладываются опять, дают неполяризованный свет. Но, если на кристалл падает поляризованный свет, то оба световых потока будут когерентными, а на выходе из кристалла при их смешивании получим эллиптически поляризованный свет. Поляризация такого света может изменяться от циркулярной (поляризация по кругу) до линейной (когда эллипс вырождается в прямую линию), в зависимости от толщины слоя, пройденного светом в кристалле,- то есть в зависимости от сдвига фаз и оптической разности хода лучей (см. лаб. раб. 62). Соответственно, кристаллическая пластинка с оптической разностью хода лучей D = l/4 ( сдвиг фаз Dj = p/2) дает циркулярно поляризованный свет и носит название пластинка в четверть волны. Пластинка в половину длины волны, соответственно, имеет Dj = p и D = l/2 и дает линейно поляризованный свет с направлением колебаний в 45° к главной оптической плоскости.
Поляризатор (анализатор), поставленный на пути такого света, пропустит колебание двух когерентных световых потоков с оптической разностью хода лучей, зависящей от толщины кристаллической пластинки. Колебания будут происходить в одном направлении, определяемом анализатором, и за ним будет наблюдаться интерференционная картина, цвет которой зависит от оптической разности хода, то есть от толщины пластинки – имеем цвета тонких кристаллических пластинок.
3.2 Экспериментальные исследования
3.2.1 Упражнение 1. Наблюдение разных типов поляризации
Материалы и принадлежности: источник обыкновенного света (проекционный фонарь), источник поляризованного света (газовый лазер), поляризаторы (2 шт.), пластинка в четверть волны, пластинка в половину длины волны, набор кристаллических пластинок разной толщины.
3.2.1.1 Порядок выполнения упражнения
1 Включить проекционный фонарь. Вращая поляризатор вокруг направления распространения света, удостовериться, что оно неполяризованное. Дать объяснение.
2 Второй поляризатор расположить за первым (сделать его анализатором). Провести наблюдение за интенсивностью света за анализатором во время его поворотов вокруг направления света. Дать объяснение.
3 Включить лазер и провести наблюдение с помощью поляризатора степени поляризации его света. Воспользоваться анализатором и сделать вывод относительно зависимости интенсивности света после анализатора от взаимного расположения поляризатора и анализатора, и их расположения относительно направления колебаний света лазера. Дать объяснение.
4 Включить настольную лампу. Взять четверть волновую пластинку и провести анализ света после нее с помощью анализатора. Провести наблюдение с помощью еще одного поляризатора, расположенного за анализатором. Сделать выводы из результатов наблюдений.
5 Взять пластинку в половину длины волны и повторить исследование п. 3.
Все результаты наблюдений и соответствующие объяснения занести к протоколу исследования.
3.2.2 Упражнение 2. Опытная проверка закона Брюстера.
1 Включить проекционный фонарь. Установить стеклянную пластинку на оптической скамье на пути света. Анализатор расположить на пути отраженного пластинкой света.
2 Изменять угол падения света на стеклянную пластинку и, вращая анализатор вокруг направления отраженного света, удостовериться в его частичной поляризации. Зафиксировать направление, в котором отраженный свет полностью поляризован. Сделать выводы относительно зависимости степени поляризации от угла падения света и относительно направления колебаний отраженного под углом Брюстера света. Занести угол Брюстера в протокол исследования и сравнить полученное значение с табличным.
3.2.3 Упражнение 3. Опытная проверка закона Малюса.
3.2.3.1 Экспериментальная установка и метод исследования
Материалы и принадлежности: источник поляризованного света (газовый лазер), анализатор в оправе со шкалой углов между направлением колебаний света и пропускным направлением анализатора, линза для рассеивания излучения лазера, приемник света (фотодиод или фоторезистор в оправе с микроамперметром) смонтированные на оптической скамье.
 |
Для опытной проверки закона Малюса (формула 3.1) используется установка, схема которой приведена на рис. 3.5.
|
3.2.3.2 Порядок выполнения работы
1 Проверить правильность расположения приборов на оптической скамье (см. рис. 3.5). Включить в сеть на 220 В блок питания лазера и питания миллиамперметра. Нажать кнопку “запуск” в блоке питания БП лазера – должно появиться излучение лазера красного цвета.
2 Установить анализатор в положение 90° и зафиксировать значение тока І90 . Занести это значение в соответствующую строчку табл. 3.1.
3 Установить анализатор в положение 0° и зафиксировать значение тока І0 . Занести это значение в табл. 3.1.
4 Провести измерения тока через каждые 15° поворота анализатора. Данные занести в табл. 3.1.
Таблица 3.1
| j,° | cos j | І, мкА | cos2j | x=(I-I90)/(I0- I90) |
| 0 | ||||
| 15 | ||||
| 30 | ||||
| 45 | ||||
| 60 | ||||
| 75 | ||||
| 90 |
3.2.3.3 Обработка результатов исследования
1 Вычислить значение cos2j и занести в соответствующий столбец табл. 3.1.
2 Вычислить значение x=(I-I90)/(I0-I90), используя соответствующие значения табл. 3.1 и учитывая, что І – текущее значение тока. Результат вычисления x занести в строку, что отвечает использованному значению I.
3 По результатами вычислений построить векторные диаграммы cos2j и x (рис. 3.6 а), откладывая их соответствующие значения на лучах, проведенных под заданными первым столбиком, углами. Или построить графики cos2j и x, как это показано на (рис. 3.6 б).
4 По результатами совпадения диаграмм (или графиков) сделать выводы относительно справедливости закона Малюса. Если такое совпадение является плохим, необходимо указать возможные причины такого результата и повторить опыты под руководством преподавателя.
|
4.3 Контрольные вопросы
1 Какова природа световых волн? Что такое световой вектор?
2 В чем заключается явление поляризации и какие волны можно поляризовать?
3 Какие виды поляризации вы знаете?
4 Как читается закон Малюса?
5 Что такое частичная поляризация света и как определяется степень его поляризации?
6 Как можно поляризовать свет? Что происходит при отражении и преломлении света на границе раздела прозрачных диэлектриков? Сформулируйте закон Брюстера.
7 Что такое двойное преломление света? Что можно сказать о поляризации обыкновенного и необыкновенного световых потоков в прозрачных кристаллах? Что можно сказать об их когерентности?
8 Что такое дихроизм веществ и что такое поляроид?
9 Как образуется циркулярно- и эллиптически-поляризованный свет?
10 Как образуются цвета кристаллических пластинок?