Примеры решения задач
Пример 1. По двум длинным прямолинейным параллельным проводникам, расстояние между которыми d = 8 см, в одном направлении текут токи I1 = 3 А, I2 = 5 А. Найти магнитную индукцию поля 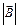 в точке А, которая находится на линии, соединяющей проводники, на расстоянии r1 = 2 см от первого проводника.
в точке А, которая находится на линии, соединяющей проводники, на расстоянии r1 = 2 см от первого проводника.
| Дано:I1 = 3 А; I2 = 5 А; d = 8 см = 8∙10-2 м; r1 = 2 см = 2∙10-2 м. Найти: ВА. |  а) б) а) б)
|
| Рис. 1 |
Решение: На рис. 1а токи I1 и I2 текут по параллельным проводникам в одном направлении перпендикулярно плоскости чертежа, от нас. Каждый из токов создаёт магнитное поле, силовые линии которого – окружности. Их направление связано с направлением тока в проводнике правилом буравчика (рис. 1б).
Согласно принципу суперпозиции результирующая индукция магнитного поля в точке А равна векторной сумме индукций 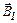 и
и 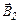 полей, создаваемых каждым током в отдельности,
полей, создаваемых каждым током в отдельности,
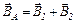 . (1)
. (1)
С учётом направления векторов 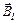 и
и 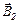 в точке А сумма их проекций на ось Оу
в точке А сумма их проекций на ось Оу
BА = B1 - B2.(2)
Значения индукций В1 и В2 в данной точкевыражаются соответственно формулами:
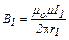 , (3)
, (3)
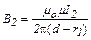 , (4)
, (4)
где m0 = 4π∙10-7 Гн/м – магнитная постоянная; m = 1 – магнитная проницаемость вакуума и воздуха.
Подставив выражения (3) и (4) для В1 и В2 в равенство (2), получим
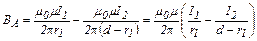 . (5)
. (5)
Вычислим искомую индукцию:
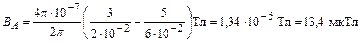 .
.
Ответ: ВА = 13,4 мкТл.
Пример 2. Определить индукцию В магнитного поля и магнитный момент Pm в центре кругового проводящего витка при разности потенциалов на его концах U = 10 В, если сопротивление проволоки витка
R = 0,5 Ом, его диаметр d = 20 см.
| Дано:R = 0,5 Ом; U = 10 В; d = 20 см = 0,2 м. Найти: B, Pm. | 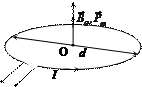
|
| Рис. 2 |
Решение: На рис. 2 показаны направления векторов 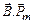 в центре кругового витка с током, найденных по правилу буравчика.
в центре кругового витка с током, найденных по правилу буравчика.
Индукция магнитного поля в центре витка определяется по формуле
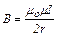 , (1)
, (1)
где I – сила тока; m0 = 4π∙10-7 Гн/м – магнитная постоянная; m = 1 – магнитная проницаемость вакуума и воздуха; r – радиус витка.
По закону Ома для участка цепи сила тока в витке
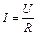 . (2)
. (2)
Подставляя (2) в (1), получим расчётную формулу для В:
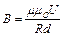 . (3)
. (3)
Вычислим индукцию в центре витка с током по формуле (3) 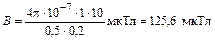 .
.
Магнитный момент Pm витка с током I находим по формуле
Pm = I∙S, (4)
где 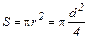 – площадь витка.
– площадь витка.
Следовательно,
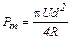 . (5)
. (5)
Вычислим магнитный момент:
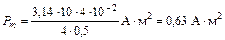 .
.
Ответ:B = 125,6 мкТл; Pm = 0,63 А∙м2.
Пример 3. Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводником так, что две её стороны параллельны проводнику. По проводнику и рамке текут одинаковые токи
I = Iр = 1 кА. Определить силу, действующую на рамку, если ближайшая к проводнику сторона рамки находится на расстоянии, равном её длине. Деформацией рамки пренебречь.
| Дано:I = Iр = 1 кА = 103 А; r1 = a; r2 = 2a. Найти: F. |
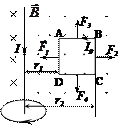 Рис. 3 Рис. 3
|
Решение: Длинный прямой проводник с током I создаёт магнитное поле, индукция B которого определим по формуле
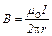 , (1)
, (1)
где mo – магнитная постоянная; r – расстояние от прямого проводника.
Согласно формуле (1) поле прямого проводника является неоднородным и ослабевает при удалении от проводника. Графически поле такого проводника изображается силовыми линиями в виде окружностей, направление которых определяется по правилу правого винта (в данном случае – по часовой стрелке) [3]. Вектор магнитной индукции 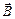 в каждой точке к силовой линии направлен по касательной. Следовательно, справа от прямого проводника векторы магнитной индукции направлены перпендикулярно плоскости чертежа, к нам (рис. 3).
в каждой точке к силовой линии направлен по касательной. Следовательно, справа от прямого проводника векторы магнитной индукции направлены перпендикулярно плоскости чертежа, к нам (рис. 3).
На каждый элемент длины 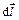 рамки АВСD, расположенной в магнитном поле проводника с током I , действует сила Ампера
рамки АВСD, расположенной в магнитном поле проводника с током I , действует сила Ампера
dFA= Iр∙B∙dl sina, (2)
где a – угол между направлениями 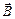 и
и 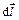 (для всех элементов
(для всех элементов 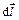 рамки a = 90o).
рамки a = 90o).
Направление сил Ампера, действующих на стороны АВ, ВС, CD, AD, определяются по правилу левой руки (рис. 3).
Сила F1, действующая на сторону АD, на основании формул (1) и (2) определяется следующим образом:
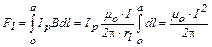 . (3)
. (3)
Аналогично получается формула для силы F2, действующей на сторону ВС, удалённую от прямого проводника на расстояние r2:
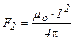 . (4)
. (4)
Силы 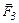 и
и 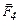 , действующие на стороны АВ и СD рамки, направлены в противоположные стороны, равны по величине и скомпенсированы, так как стороны АВ и СD расположены одинаково относительно прямого проводника.
, действующие на стороны АВ и СD рамки, направлены в противоположные стороны, равны по величине и скомпенсированы, так как стороны АВ и СD расположены одинаково относительно прямого проводника.
Равнодействующая всех сил, приложенных к рамке,
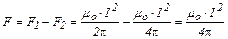 .(5)
.(5)
Значение силы 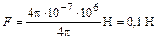 .
.
Ответ: F = 0,1 Н.
Пример 4. В масс-спектрометре пучок ионов проходит ускоряющую разность потенциалов U = 10 кВ и попадает в однородное поперечное магнитное поле с индукцией В = 100 мТл. Направление вектора скорости 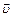 после прохождения магнитного поля по дуге окружности меняется на противоположное. Найти расстояние между входной щелью приёмника и выходной щелью ускоряющей камеры. Отношение заряда иона q к его массе m (удельный заряд) считать известным и равным
после прохождения магнитного поля по дуге окружности меняется на противоположное. Найти расстояние между входной щелью приёмника и выходной щелью ускоряющей камеры. Отношение заряда иона q к его массе m (удельный заряд) считать известным и равным
q/m =3,2∙107 Кл/кг. Действием силы тяжести пренебречь, считать начальную скорость ионов uo = 0.
Дано:U = 10 кВ = 104 В;
В = 100 мТл = 0,1 Тл;
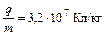 .
uo = 0.
Найти: d. .
uo = 0.
Найти: d.
|  Рис. 4 Рис. 4
|
Решение: При прохождении ускоряющей разности потенциалов U работа сил электростатического поля приводит к изменению кинетической энергии ионов:
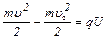 . (1)
. (1)
С учётом того, что скорость, с которой ионы влетают в магнитное поле, u0 = 0:
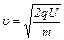 . (2)
. (2)
Со стороны магнитного поля на движущиеся ионы действует сила Лоренца
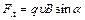 , (3)
, (3)
где a = 90о – угол между векторами 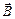 и
и 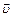 .
.
Направление силы Лоренца определяется по правилу левой руки (рис. 4). Так как вектор силы 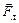 перпендикулярен вектору скорости
перпендикулярен вектору скорости 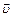 , то модуль скорости не изменяется. Сила Лоренца сообщает ионам центростремительное ускорение:
, то модуль скорости не изменяется. Сила Лоренца сообщает ионам центростремительное ускорение:
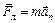 . (4)
. (4)
Тогда
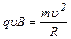 , (5)
, (5)
где R – радиус кривизны траектории.
Используя формулу (2), получим
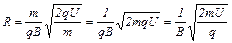 . (6)
. (6)
По условию задачи направление вектора скорости 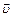 при попадании на фотопластинку приёмника противоположно направлению скорости
при попадании на фотопластинку приёмника противоположно направлению скорости 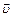 при входе в магнитное поле. Поэтому искомое расстояние d = 2R.
при входе в магнитное поле. Поэтому искомое расстояние d = 2R.
Формула для d имеет вид: 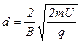 . (7)
. (7)
Отсюда 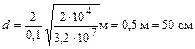 .
.
Ответ: d = 50 см.
Пример 5. На квадратную рамку со стороной а = 10 см, помещенный между полюсами постоянного магнита, действует максимальный механический момент Мmax = 6,5 мкНм, если в рамке сила тока I = 2 А. Определить магнитную индукцию В между полюсами магнита. Действием магнитного поля Земли пренебречь.
| Дано:а = 10 см = 0,1 м; Мmax = 6,5 мкНм = 6,5∙10-6 Нм; I = 2 А. Найти: В. | 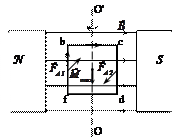 Рис. 5 Рис. 5
|
Решение:На рис. 5 изображена рамка с током (ток направлен по часовой стрелке) в магнитном поле магнита. На стороны fb и cd действуют силы Ампера 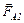 и
и 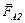 , равные по величине, противоположные по направлению и создающие вращающий момент М относительно
, равные по величине, противоположные по направлению и создающие вращающий момент М относительно
оси ОО¢:
M = Pm B sina, (1)
где Pm – магнитный момент рамки с током; a – угол между векторами 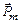 и
и 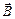 .
.
Вектор 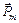 в центре рамки направлен перпендикулярно чертежу (по правилу буравчика), от нас, и его модуль
в центре рамки направлен перпендикулярно чертежу (по правилу буравчика), от нас, и его модуль
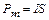 , (2)
, (2)
где S = а2 – площадь рамки.
Вращающий момент принимает максимальное значение при a = 90o
Mmax = Pm∙B = = I a2 B. (3)
Откуда
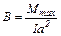 . (4)
. (4)
Магнитная индукция поля магнита  .
.
Ответ:В = 32,5 мкТл.
Пример 6. Катушка длиной l = 50 см и площадью сечения S = 30 см2 имеет 12 витков на 1 см длины. Индукция магнитного поля в катушке
В = 8 мТл. Определить: силу тока I; индуктивность L; энергию магнитного поля W катушки.
| Дано:l = 50 см = 0,5 м; S = 30 cм2 = 3∙10-3 м; n = 12 см-1 = 1200 м-1; В = 8 мТл = 8∙10-3 Тл. Найти: I; L; W. |   Рис. 6
Рис. 6
|
Решение:На рис. 6 показано направление тока в катушке, а также направление силовых линий созданного током магнитного поля. Для длинного соленоида, каковым является предлагаемая катушка с током, индукция магнитного поля
В = mo m n I , (1)
где mo = 4π∙10-7 Гн/м – магнитная постоянная; m – магнитная проницаемость среды (сердечника), для воздуха m = 1; n – плотность витков.
Из формулы (1) имеем
 . (2)
. (2)
Определим значение силы тока в катушке:
 .
.
Индуктивность соленоида находим по формуле
 . (3)
. (3)
Отсюда L = 4∙3,14∙10-7∙1,22∙106∙3∙10-3∙0,5 Гн = 2,7 мГн.
Энергия магнитного поля катушки:
 . (4)
. (4)
Величина энергии  .
.
Ответ: I = 5,3 А; L = 2,7 мГн; W= 38 мДж.
Пример 7.В однородном магнитном поле, индукция которого
Во = 250 мТл, находится плоская катушка радиусом R = 25 см, содержащая N = 75 витков. Плоскость катушки составляет угол g = 600 с направлением вектора индукции. По виткам течёт ток силой I = 3 А. Определить магнитный поток Фо и потокосцепление yо в катушке. Какую работу надо совершить, чтобы удалить катушку из магнитного поля?
| Дано:Во = 250 мТл = 0,25 Тл; N =75 витков; R = 25 см = 0,25 м; g = 60o; I = 3 А; В = 0. Найти: Фо; yо; Авнеш. |  Рис. 7
Рис. 7
|
Решение:В случае однородного магнитного поля магнитный поток через плоский контур площадью S определяется по формуле
Фо = Во S cosa, (1)
где a – угол между вектором нормали  к плоскости контура и вектором
к плоскости контура и вектором  , S = πR2 – площадь одного витка.
, S = πR2 – площадь одного витка.
Согласно рис. 7
 . (2)
. (2)
Учитывая (2), формула (1) примет вид
 . (3)
. (3)
Отсюда  .
.
Потокосцепление, т.е. полный магнитный поток, сцепленный со всеми витками катушки,
yо = N Фо. (4)
Следовательно, yо = 75∙0,042 = 3,15 Вб.
Работа магнитного поля по перемещению катушки определяется формулой
А = I (y – yо). (5)
Чтобы удалить катушку из поля, к ней надо приложить внешнюю, например, механическую силу, работа которой
Авнеш = – А = I (yо – y), (6)
где y = 0, так как В = 0.
Подставляя yо и y в формулу (6), получим Авнеш = 9,45 Дж.
Ответ: Фо = 42 мВб; yо = 3,15 Вб; Авнеш = 9,45 Дж.
Пример 8.В однородном магнитном поле индукцией В = 100 мТл равномерно вращается с частотой n = 10 с-1 рамка, содержащая
N = 1000 витков. Площадь рамки S = 150 см2. Определить амплитудное значение эдс εmax и мгновенное значение эдс ε, соответствующее углу поворота рамки a = 300.
| Дано:В = 100 мТл = 0,1 Тл; N =1000; S = 150 см2= 15∙10-3 м2; a = 30o; n = 10 с-1. Найти: ε; εmax. |
Решение: При вращении рамки площадью S в магнитном поле индукцией В поток Ф изменяетсяпо закону
Ф = В S coswt, (1)
где  – угловая скорость.
– угловая скорость.
Мгновенное значение эдс индукции ε определяется основным уравнением электромагнитной индукции Фарадея–Максвелла
 , (2)
, (2)
где y = N Ф – потокосцепление.
Следовательно,
 . (3)
. (3)
Подставив (1) в (3), получим выражение для мгновенного значения эдс, наведённой в рамке,
 . (4)
. (4)
Амплитудное значение эдс emax найдём из выражения (4):
εmax∙= 2πnNBS. (5)
Отсюда εmax∙= 2∙3,14∙1000∙0,1∙15∙10-3∙10 В = 94,2 В.
Мгновенное значение эдс индукции при a = 30 o
 .
.
Ответ:ε = 47,1 В; εmax∙= 94,2 В.
Пример 9. Квадратная проволочная рамка со стороной а = 5 см и сопротивлением R = 10 мОм находится в однородном магнитном поле
индукцией В = 40 мТл. Нормаль к плоскости рамки составляет угол
a = 30o с линиями магнитной индукции. Определить заряд q, который пройдёт по рамке, если магнитное поле выключить.
| Дано:В = 40 мТл = 4∙10-2 Тл; R = 10 мОм= 10-2 Ом; a = 30o; а = 5 см = 5∙10-2 м. Найти: q. |
 Рис. 9 Рис. 9
|
Решение:В начальный момент временизначение магнитного потока через рамку
Ф1 = В×S cos a= B×a2 cosa. (1)
При выключении магнитного поля произойдёт изменение магнитного потока от значения Ф1 до значения Ф2 = 0. Вследствие этого в рамке возбуждается эдс, определяемая основным законом электромагнитной индукции:
 . (2)
. (2)
В рамке возникнет кратковременный ток (его направление указано на рис. 9 согласно правилу Ленца). Мгновенное значение силы тока находим по закону Ома для замкнутой цепи
 . (3)
. (3)
Из (1) и (2) имеем
 . (4)
. (4)
По определению сила тока
 . (5)
. (5)
Подставив (4) в (3), приходим к выражению
 . (6)
. (6)
Интегрируя выражение (5), получим величину заряда, который пройдёт по рамке при выключении магнитного поля:
 , (7)
, (7)
откуда
 . (8)
. (8)
Подставив (1) в выражение (8), получаем искомую формулу для заряда:
 . (9)
. (9)
Значение заряда  .
.
Ответ: q = 8,66 мКл.