СПЕКТРЫ ПРИ УГЛОВОЙ МОДУЛЯЦИИ

 

При анализе спектров ограничимся рассмотрением простей­шего случая угловой модуляции по гармоническому закону. Как при ЧМ, так и при ФМ выражения (15.48) и (15.56) для этого случая можно свести к виду

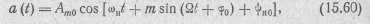
где m = m_ω, при ЧМ и т = т_ψ при ФМ.

Перепишем его в более удобном для анализа виде

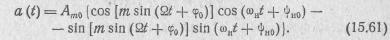
Из теории функций Бесселя известно, что

где через J_n(x) обозначена функция Бесселя первого рода «-го порядка аргумента х.

Применяя эти соотношения, положив y=Ωt+φ₀ и х = т, после несложных преобразований получаем

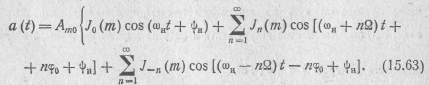
Из теории функций Бесселя известно также, что

.(15.64)

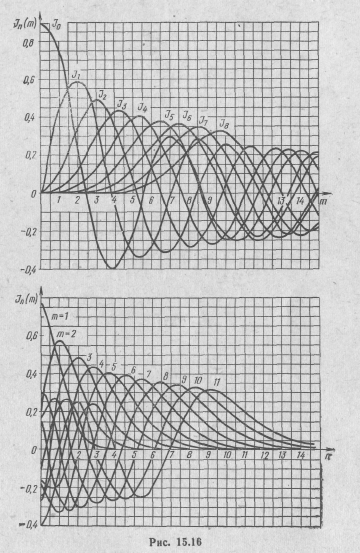
Значения функций Бесселя известны в виде таблиц и графиков (рис. 15.16). Они могут быть вычислены и с помощью разложения в степенной ряд.

Из выражения (15.63) следует, что спектр ЧМ или ФМ коле­бания даже в случае простейшей гармонической модуляции имеет бесконечное множество гармоник, образующих верхнюю и ниж-

нюю боковые полосы, с частотами ω_н+nΩ, и ω_н-nΩ. В слу­чае АМ колебаний при этом имеют место лишь две боковые со­ставляющие,

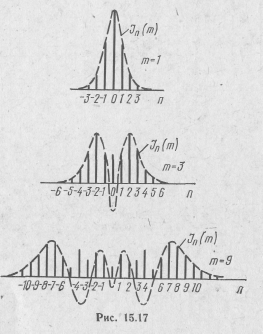
Амплитуда каждой гармонической составляющей частоты ω_н±nΩ в спектре ЧМ и ФМ колебания определяется абсолютным значением функции Бесселя n-го порядка с аргументом m=m_ψ=m_ω и может быть вычислена с помощью кривых или таблиц этих функций. Амплитуды составляющих изменяются в за­висимости от индекса модуляции т. В качестве примера на рис. 15.17 приведены спектры ЧМ колебания при разных значе­ниях т.

Анализ спектров показывает, что с увеличением индекса m порядок составляющих с максимальной амплитудой увеличи­вается, стремясь к т. При этом составляющие высшего порядка приобретают все большее относительное значение. С возраста­нием т энергия модулированного сигнала сосредоточивается в со­ставляющих высокого порядка. Простые количественные измене­ния индекса модуляции, пропорционального интенсивности моду­лирующего сигнала, при угловой модуляции приводят к значитель­ным качественным изменениям спектра. Это объясняется следую­щим образом. Если при АМ энергия боковых гармонических со­ставляющих возникает за счет изменения амплитуды колебания, то при угловой модуляции амплитуда неизменна и их энергия мо­жет быть получена лишь за счет энергии составляющей несущей

частоты. Поэтому чем больше т, тем сильнее подчеркиваются удаленные боковые частоты и уменьшаются амплитуды несущей и ближайших к ней гармонических составляющих.

Теоретически спектр сигнала при угловой модуляции является бесконечным, но на практике его можно считать ограниченным. Объясняется это тем, что при заданном т значения функций Бесселя J_n(m) при значительном увеличении их порядка п быстро уменьшаются. Как видно из графиков (15.16,6), начиная с 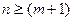, значения J_n(m) становятся весьма малыми. Поэтому гармоническими составляющими с порядковыми номерами 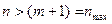в разложении (15.63) практически можно пре­небречь.

Обозначим максимальный порядковый номер учитываемой со­ставляющей через 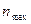. Тогда ширина спектра модулированного колебания составит

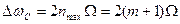(15.65)

или для значений т>>1

. (15.66)

Ширина спектра при угловой модуляции в зависимости от ее вида определяется девиацией фазы или частоты.

В свое время среди радиотехников было распространено мне­ние, что при ЧМ с небольшой девиацией частоты можно сузить полосу частот, занимаемую радиосигналом, в сравнении с систе­мой АМ. Прочность этого заблуждения, известного как «парадокс узкополосной ЧМ», можно пояснить выдачей в 30-х годах патента США на его использование.

Предположим, что m<<l. Тогда

т. е. в спектре кроме колебания основной частоты ω_н следует учи­тывать только первую пару боковых частот |ω_н±Ω|. Отсюда ши­рина спектра

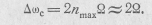
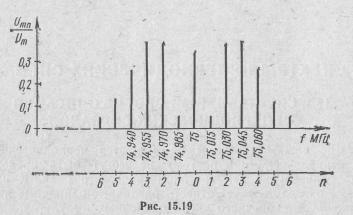
Таким образом, при угловой модуляции с малыми индексами модуляции (узкополосная ЧМ) ширина спектра колебания совп дает с шириной спектра при АМ. При малых т амплитудно-частотные спектры ФМ, ЧМ и АМ колебаний практически совпадают. Разница в спектрах возрастает при больших индексах модуляции (широкополосная ЧМ). В радиовещательных систем ЧМ девиация частоты обычно выбирается равной 75 кГц. При частоте модуляции F=lкГц этому соответствует индекс модулящ

т_ω = 75/1 = 75и ширина спектра 150 кГц. В случае амплитудной модуляции ширина спектра оказывается равной лишь 2 кГ

Передача широкополосных ЧМ и ФМ сигналов практически воз­можна только в диапазоне ультракоротких волн (УКВ).

Сравнение спектра ФМ и ЧМ колебаний (рис. 15.18) показы­вает, что при одинаковых ω_н, Ω и т их спектры ничем не отли-

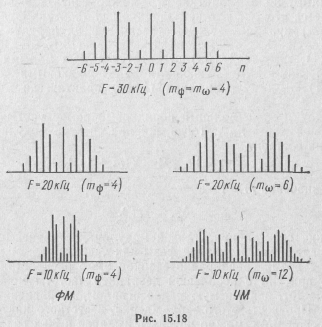
чаются. Изменения ω_н и т вызывают одинаковые изменения в спектрах ФМ и ЧМ колебаний.

Отличительной особенностью спектра ЧМ колебания в сравне­нии с ФМ является практически независимость его ширины от частоты модуляции. При ЧМ с уменьшением Ω индекс модуляции увеличивается пропорционально Ω, а ширина спектра

остается неизменной. Действительно, с уменьшением Ω расстояние между спектральными линиями также уменышется, но при ЧМ это сопровождается ростом т, что в свою очередь приводит к уве­личению числа учитываемых гармоник. В результате ширина спектра практически не изменяется.

В случае же ФМ индекс модуляции т_ψ=Δψ не зависит от Ω. Поэтому с изменением Ω число учитываемых гармоник остается неизменным, а ширина спектра меняется:

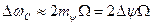. (15.68)

Таким образом, ЧМ в отличие от ФМ характеризуется боль­шим постоянством спектров сигналов, что является одной из при-

чин предпочтительного применения ЧМ на практике. ФМ и ЧМ колебания по сравнению с АМ занимают более широкую полосу частот, но обладают двумя важными преимуществами: высокой помехоустойчивостью и возможностью обеспечить передачу более мощного сигнала при равной мощности радиопередатчика,

ЧМ осуществляется в генераторах на клистронах, лампах бе­гущей волны (ЛБВ), лампах обратной волны (ЛОВ), магнетро­нах, платинотронах, в схемах с реактивной лампой и др.