Линии второго порядка

1.40. Составить уравнение окружности с центром в точке (1;2) и проходящей через точку (-3;-4).

1.41. Составить уравнение окружности, зная, что она проходит через точки А(0;1), B(-2;0), C(2;0).

1.42. Найти уравнение прямой которая проходит через центр окружности x²+ y² -4x - 3y + 6 = 0 параллельно прямой 2x - y - 4 = 0

1.43. Дана окружность х² + у² = 4. Из ее точки А (2;0) проведены всевозможные хорды. Определить геометрическое место середин этих хорд.

1.44. Определить длину хорды окружности (х + 2)² + (у + 4)² = 10, делящейся в точке А (-1;-2) пополам.

1.45. Найти длину хорды окружности (х - 2)² + у² = 2, если известно уравнение хорды у = -1

1.46. Найти уравнение окружности, касающейся осей координат, если центр лежит в точке с координатами (a; -а)

1.47. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, кроме того, что

1) его полуоси равны 6 и 4,

2) его большая ось равна 20, а расстояние между фокусами 2с=12,

3) его малая ось равна 24 а расстояние между фокусами 2с=16,

4) расстояние между его фокусами равно 16 и эксцентриситет ,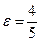

5) его большая ось равна 10, а эксцентриситет ,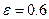

6) его малая полуось равна 10, а эксцентриситет ,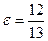

7) расстояние между его директрисами равно 10 и рассояние между фокусами 2с=8,

8) его боьшая ось равна 8, а расстояние между директрисами равно 16,

9) его малая ось равна 4 расстояние между директриссами равно 10,

10) расстояние между его директрисами равно 16 и .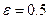

1.48. Дан эллипс 2х² + 3у² = 18 найти:

1) его полуоси,

2) фокусы,

3) эксцентриситет,

4) уравнение директрис.

1.49. Определить траекторию точки М, которая при своем движении остается вдвое ближе к точке А(2;-2), чем к прямой х+1=0

1.50. Составить уравнение линии, сумма расстояний точек которой до точек А (2;4) и В (-4;4) равно 8.

1.51. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:

1) ее оси 2а=4 и 2b=6,

2) расстояние между фокусами 2с=16 и ось 2b=12,

3) расстояние между фокусами 2с=6 и эксцентриситет ,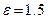

4) ось 2а=12 и эксцентриситет ,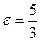

5) уравнение ассимптот и расстояние между фокусами ,

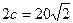6) расстояние между директрисами равно 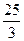и расстояние между фокусами 2с=48,

7) расстояние между директрисами равно 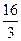и ось ,

8) расстояние между директрисами равно 7,2, а эксцентриситет ,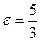

9) уравнение асимптот 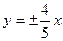и расстояние между директрисами равно .

1.52. Найти острый угол между асимптотами гиперболы х² - 3у² = 27.

1.53. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:

1) парабола расположена симметрично относительно оси Оx и проходит через точку А(3;6),

2) парабола расположена в правой полуплоскости симметрично относительно оси Оx и ее параметр р=5,

3) парабола расположена в верхней полуплоскости симметрично оси Оy, и ее параметр р=2,

4) парабола расположена в нижней полуплоскости симметрично оси Оy, и ее параметр р=1,5,

5) парабола расположена в левой полуплоскости симметрично оси Оx, и ее параметр р=2,5.

1.54. Составить уравнение геометрического места точек, одинаково удаленных от точки F(0;1) и от прямой у=3.

1.55. Найти координаты вершины параболы, заданной уравнением
х = 2у² + 4у-5. Написать уравнение оси симметрии параболы.

1.56. Найти координаты фокуса параболы

1) у²=4х,

2) х²=8у,

3) у²=-4х,

4) х²=-2у.